题目内容
 一副三角板按如图所示放置,其中∠F=∠ACB=90°,∠E=30°,∠A=45°,点C在FD的延长线上,点B在DE上.
一副三角板按如图所示放置,其中∠F=∠ACB=90°,∠E=30°,∠A=45°,点C在FD的延长线上,点B在DE上.(1)当AB∥CF时,求∠DBC的度数;
(2)当AB∥CF时,且AB=24时,求CD的长.
考点:勾股定理,平行线的性质
专题:
分析:(1)根据三角形内角和定理求出∠BDF和∠ABC,根据平行线性质求出∠ABD,即可得出答案;
(2)过B作BM⊥DF于M,解直角三角形求出BC=AB×sin45°=12
,在Rt△BMC中,解直角三角形求出BM=CM=12,OM=4
,即可得出答案.
(2)过B作BM⊥DF于M,解直角三角形求出BC=AB×sin45°=12
| 2 |
| 3 |
解答:解:(1)∵∠F=90°,∠E=30°,
∴∠EDF=60°,
∵∠BCA=90°,∠A=45°,
∴∠ABC=45°,
∵AB∥FC,
∴∠BAD=∠EDF=60°,
∴∠DBC=60°-45°=15°;
(2)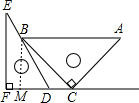
过B作BM⊥DF于M,
∵在Rt△ACB中,∠BCA=90°,∠A=45°,AB=24,
∴BC=AB×sin45°=12
,
∵在Rt△BMC中,∠BCM=∠BDM-∠DBC=60°-15°=45°,
∴BM=CM=BC×sin45°=12,
∵在Rt△BDM中,∠BDM=60°,∠BMD=90°,BM=12,
∴DM=
=4
,
∴CD=CM-DM=12-4
.
∴∠EDF=60°,
∵∠BCA=90°,∠A=45°,
∴∠ABC=45°,
∵AB∥FC,
∴∠BAD=∠EDF=60°,
∴∠DBC=60°-45°=15°;
(2)

过B作BM⊥DF于M,
∵在Rt△ACB中,∠BCA=90°,∠A=45°,AB=24,
∴BC=AB×sin45°=12
| 2 |
∵在Rt△BMC中,∠BCM=∠BDM-∠DBC=60°-15°=45°,
∴BM=CM=BC×sin45°=12,
∵在Rt△BDM中,∠BDM=60°,∠BMD=90°,BM=12,
∴DM=
| BM |
| tan45° |
| 3 |
∴CD=CM-DM=12-4
| 3 |
点评:本题考查了勾股定理,解直角三角形,平行线的性质等知识点的应用,能综合运用性质进行推理和计算是解此题的关键,有一定的难度.

练习册系列答案
相关题目
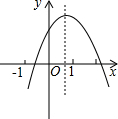 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①abc>0 ②2a+b<0 ③4a-2b+c<0 ④
| 4ac-b2 |
| 4a |
其中正确结论的个数为( )
| A、4个 | B、3个 | C、2个 | D、1个 |
能同时把矩形的面积和周长分成相等两部分的直线有( )条.
| A、1条 | B、2条 | C、3条 | D、无数条 |
 如图所示,把一张长方形的纸片沿着AB折叠,若∠1=50°.则∠2的度数为( )
如图所示,把一张长方形的纸片沿着AB折叠,若∠1=50°.则∠2的度数为( )| A、40° | B、50° |
| C、65° | D、75° |

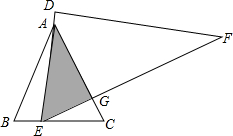 如图,等边△ABC中,AB=6,将一直角三角板DEF的60°角的顶点E置于边BC上移动(不与B、C重合),移动过程中,始终满足直角边DE经过点A,斜边EF交AC于点G.
如图,等边△ABC中,AB=6,将一直角三角板DEF的60°角的顶点E置于边BC上移动(不与B、C重合),移动过程中,始终满足直角边DE经过点A,斜边EF交AC于点G.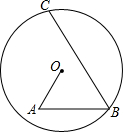 如图,在圆O中,点A在圆内,B,C在圆上,其中OA=7,BC=18,∠A=∠B=60°,则OB=
如图,在圆O中,点A在圆内,B,C在圆上,其中OA=7,BC=18,∠A=∠B=60°,则OB= 如图所示,已知AB=AC,BD=CD,BC,AD相交于O,则AD⊥BC,你认为这个结论对吗?
如图所示,已知AB=AC,BD=CD,BC,AD相交于O,则AD⊥BC,你认为这个结论对吗? 如图,在△ABC中,点D在BC上,BD:DC=1:2,点E在AB上,AE:EB=3:2,AD,CE相交于F,则AF:FD=
如图,在△ABC中,点D在BC上,BD:DC=1:2,点E在AB上,AE:EB=3:2,AD,CE相交于F,则AF:FD=