题目内容
8.若等边△ABC的边长为4cm,那么△ABC的面积为( )| A. | 2$\sqrt{3}$cm2 | B. | 4$\sqrt{3}$cm2 | C. | 6$\sqrt{3}$cm2 | D. | 8cm2 |
分析 根据等边三角形三线合一的性质,根据勾股定理即可求AD的值,根据AD、BC即可计算△ABC的面积.
解答  解:∵等边三角形三线合一,
解:∵等边三角形三线合一,
∴D为BC的中点,
∴BD=DC=2cm,AB=4cm,
在Rt△ABD中,AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=2$\sqrt{3}$cm,
∴△ABC的面积为$\frac{1}{2}$BC•AD=$\frac{1}{2}$×4×2$\sqrt{3}$cm2=4$\sqrt{3}$cm2,
故选B.
点评 本题考查了等边三角形三线合一的性质,考查了勾股定理在直角三角形中的运用,考查了三角形面积的计算,本题中根据勾股定理计算AD的长是解题的关键.

练习册系列答案
相关题目
13.下列各组二次根式,经化简后可以合并的是( )
| A. | $\sqrt{12}$与$\sqrt{24}$ | B. | $\sqrt{18}$与$\sqrt{24}$ | C. | $\sqrt{8}$与$\sqrt{18}$ | D. | $\sqrt{45}$与$\sqrt{12}$ |
20. 如图,△ABC中,∠A=52°,O是边AB和边AC的垂直平分线的交点,那么∠OCB=( )
如图,△ABC中,∠A=52°,O是边AB和边AC的垂直平分线的交点,那么∠OCB=( )
 如图,△ABC中,∠A=52°,O是边AB和边AC的垂直平分线的交点,那么∠OCB=( )
如图,△ABC中,∠A=52°,O是边AB和边AC的垂直平分线的交点,那么∠OCB=( )| A. | 36° | B. | 120° | C. | 38° | D. | 76° |
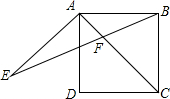 如图,在正方形ABCD中,AE=AD,∠DAE=60°,BE交AC于点F.
如图,在正方形ABCD中,AE=AD,∠DAE=60°,BE交AC于点F.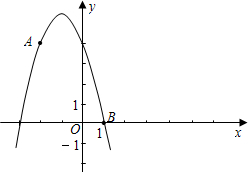 如图,已知A(-2,4)和B(1,0)都在抛物线$y=-\frac{4}{3}{x^2}-\frac{8}{3}x+4$
如图,已知A(-2,4)和B(1,0)都在抛物线$y=-\frac{4}{3}{x^2}-\frac{8}{3}x+4$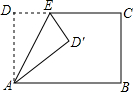 将长方形ABCD沿AE折叠,得到如图所示的图形,若∠CED′=50°,则∠EAB的大小是65°.
将长方形ABCD沿AE折叠,得到如图所示的图形,若∠CED′=50°,则∠EAB的大小是65°.