题目内容
17.化简($\sqrt{5}$-2)2015•($\sqrt{5}$+2)2016=$\sqrt{5}$+2.分析 先利用积的乘方得到原式=[($\sqrt{5}$-2)($\sqrt{5}$+2)]2015•($\sqrt{5}$+2),然后利用平方差公式计算.
解答 解:原式=[($\sqrt{5}$-2)($\sqrt{5}$+2)]2015•($\sqrt{5}$+2)
=(5-4)2015•($\sqrt{5}$+2)
=$\sqrt{5}$+2.
故答案为$\sqrt{5}$+2.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.若等边△ABC的边长为4cm,那么△ABC的面积为( )
| A. | 2$\sqrt{3}$cm2 | B. | 4$\sqrt{3}$cm2 | C. | 6$\sqrt{3}$cm2 | D. | 8cm2 |
5.下列各式(1)b5•b5=2b5(2)(-2a2)2=-4a4(3)(an-1)3=a3n-1(4)a2+a3=a5(5)2m+3n=6m+n(6)(a-b)5(b-a)4=(a-b)(7)-a3•(-a)5=a8,其中计算错误的有( )
| A. | 6个 | B. | 5个 | C. | 4个 | D. | 7个 |
2.下列二次根式中属于最简二次根式的是( )
| A. | $\sqrt{24}$ | B. | $\sqrt{13}$ | C. | $\sqrt{\frac{a}{b}}$ | D. | $\sqrt{4a+4}$ |
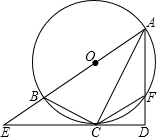 如图,已知AB为⊙O的直径,AD⊥EC于点D且交⊙O于点F,且BC=CF.
如图,已知AB为⊙O的直径,AD⊥EC于点D且交⊙O于点F,且BC=CF. 如图,将三角形ABC沿着DE折叠,使点A落在BC上的点F处,且DE∥BC,若∠B=70°,则∠BDF=40°.
如图,将三角形ABC沿着DE折叠,使点A落在BC上的点F处,且DE∥BC,若∠B=70°,则∠BDF=40°.