题目内容
中心对称图形和旋转对称图形的区别是什么呢？
见解析
【解析】【试题分析】注意从定义上区别.
【试题解析】中心对称是把一个图形绕其几何中心旋转180度后能够和原来的图形互相重合的图形叫中心对称图形.这个点就是它的对称中心．例如菱形；旋转对称不是旋转一定的角度，而是旋转非周角的角度。就是说不能是旋转360度的整数倍后与自身重合了。例如电扇的叶片转动120°与自身重合，当然菱形也是旋转对称，但并不是所有的旋转对称都是中心对称.
...
练习册系列答案
相关题目
如图，在△ABC中，CA=CB，AD⊥BC，BE⊥AC，AB=5，AD=4，则AE=__．
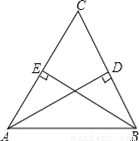
3
【解析】试题分析：∵在△ABC中，CA=CB，AD⊥BC，BE⊥AC，∴△ABD≌△BAE（AAS）。∴AD=BE=4。
∵AB=5，∴。 如图，转动转盘，指向阴影部分的可能性为a，指向空白部分的可能性为b，则（ ）
A. a＞b B. a＜b C. a=b D. 无法确定
C
【解析】由图可知，阴影部分与空白部分的面积相等，故a=b.
故选C. 如图，在△ABC中，AB＝AC，∠BAC＝120°，AB的垂直平分线交AB于点E，交BC于点F.若BF＝3cm.求BC.
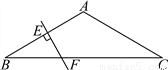
9cm
【解析】试题分析：先根据等腰三角形性质和三角形内角和定理求出∠B=∠C=30°，根据线段垂直平分线性质和等腰三角形性质求出∠BAF=30°，根据含30度角的直角三角形性质求出AF、FC即可．
试题解析：
∵在△ABC中，AB=AC，∠A=120°，
∴∠B=∠C=30°，
∵AB的垂直平分线EF，
∴AF=BF，
∴∠BAF=∠B=30°，
又∵BF=3... 如图，在△ABC中，AB＝AC，∠A＝120°，BC＝6cm，AB的垂直平分线交BC于点M，交AB于点E，AC的垂直平分线交BC于点N，交AC于点F，则MN的长为( )
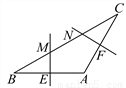
A. 4cm B. 3cm C. 2cm D. 1cm
C
【解析】连接AM、AN、过A作AD⊥BC于D，如图所示：
∵在△ABC中，AB=AC，∠A=120°，BC=6cm，
∴∠B=∠C=30°，BD=CD=3cm，
∴AB= cm=AC，
∵AB的垂直平分线EM，
∴BE= AB= cm
同理CF=cm，
∴BM==2cm，
同理CN=2cm，
∴MN=BC-BM-CN=2cm，
故选C． 判断对错：轴对称图形也是中心对称图形；__________________
错
【解析】有的图形是轴对称图形但不一定是中心对称图形，例如等腰三角形.
故答案：错. 圆是中心对称图形，它的对称中心是( )
A. 圆周 B. 圆心 C. 半径 D. 直径
B
【解析】圆的是既是中心对称图形又是轴对称图形，对称中心是圆心.故选B. 若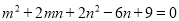
，则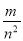
的值为______________
【解析】∵m2+2mn+2n2-6n+9=0
∴（m+n）2+（n-3）2=0，
∴m+n=0且n-3=0，
∴m=-3，n=3，
∴，
故答案为-. 将点A(1，－3)沿x轴向左平移3个单位长度，再沿y轴向上平移5个单位长度后得到的点A′的坐标为____．
(－2，2)．
【解析】∵点A（1，﹣3）沿x轴向左平移3个单位长度，再沿y轴向上平移5个单位长度后得到点A′，∴点A′的横坐标为1﹣3=﹣2，纵坐标为﹣3+5=2，∴A′的坐标为（﹣2，2）．故答案为：（﹣2，2）．