题目内容
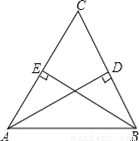
如图，在△ABC中，CA=CB，AD⊥BC，BE⊥AC，AB=5，AD=4，则AE=__．
3
【解析】试题分析：∵在△ABC中，CA=CB，AD⊥BC，BE⊥AC，∴△ABD≌△BAE（AAS）。∴AD=BE=4。
∵AB=5，∴。
练习册系列答案
相关题目
如果关于x的不等式(3m－1)x＞3m－1的解集为x＜1，那么m的取值范围是( )
A. m＞
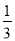B. m＜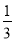
C. m＞－
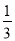D. m＜－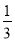
B
【解析】根据一元一次不等式的解法和基本性质，可由关于x的不等式(3m－1)x＞3m－1的解集为x＜1，可知3m-1＜0，解得m＜.
故选：B. 分式x-y+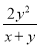
的值为（ ）
A.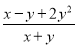 
B. x+y C. 
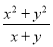D. 以上都不对
C
【解析】试题分析：原式＝
＝
＝．
故选C． 下列说法正确的是( )
A. “任意画一个三角形,其内角和为360°”是随机事件
B. 已知某篮球运动员投篮投中的概率为0.6,则他投10次可投中6次
C. 抽样调查选取样本时,所选样本可按自己的喜好选取
D. 检测某城市的空气质量,采用抽样调查法
D
【解析】试题解析：A、“任意画一个三角形，其内角和为360°”是不可能事件，故A错误；
B、已知某篮球运动员投篮投中的概率为0.6，则他投十次可能投中6次，故B错误；
C、抽样调查选取样本时，所选样本要具有广泛性、代表性，故C错误；
D、检测某城市的空气质量，采用抽样调查法，故D正确；
故选：D． 如图，BC=4cm，AB=3cm，AF=12cm，AC⊥AF，正方形CDEF的面积是169cm2，试判断△ABC的形状？
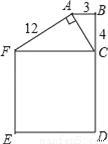
△ABC是直角三角形.
【解析】分析：首先根据正方形的面积求出FC的长，再在Rt△ACF中利用勾股定理求出AC的长，然后根据勾股定理逆定理证明∠B=90°即可．
本题解析：
∵正方形CDEF的面积是169 cm2，
∴FC=13 cm
在Rt△ACF中，由勾股定理得，
AC2=CF2﹣AF2=132﹣122=25，
在△ABC中，因为AB2+BC2=32+... 在平行四边形ABCD中，E是AD上一点，AE=AB，过点E作直线EF，在EF上取一点G，使得∠EGB=∠EAB，连接AG．
（1）如图①，当EF与AB相交时，若∠EAB=60°，求证：EG=AG+BG；
（2）如图②，当EF与CD相交时，且∠EAB=90°，请你写出线段EG、AG、BG之间的数量关系，并证明你的结论．
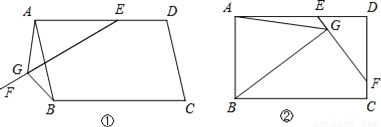
（1）证明见解析；（2）EG=AG﹣BG，理由见解析．
【解析】试题分析：（1）如图，作∠GAH=∠EAB交GE于点H，易证△ABG≌△AEH ，再判定△AGH是等边三角形，即可得结论；（2）EG=AG-BG，如图②，作∠GAH=∠EAB交GE于点H，类比（1）的方法证明△ABG≌△AEH，再判定△AGH是等腰直角三角形，即可得结论.
试题解析：
如图，作∠GAH=∠EAB交GE... 已知平行四边形ABCD中，∠B=4∠A，则∠C=__．
36°
【解析】试题解析：∵四边形BCDA是平行四边形，
∴AD∥CB，∠A=∠C，
∴∠A+∠B=180°，
∵∠B=4∠A，
∴∠A+4∠A=180°，
解得：∠A=36°，
∴∠C=36°. 同时掷两枚质地均匀的正方体骰子，骰子的六个面上分别刻有1到6的点数，下列事件中是不可能发生的事件是( )
A. 点数之和为12 B. 点数之和小于3 C. 点数之和大于4且小于8 D. 点数之和为13
D
【解析】试题分析：找到一定不会发生的事件即可．
【解析】
A、6点+6点=12点，为随机事件，不符合题意；
B、例如：1点+1点=2点，为随机事件，不符合题意；
C、例如：1点+5点=6点，为随机事件，不符合题意；
D、两枚骰子点数最大之和为12点，不可能是13点，为不可能事件，符合题意．
故选：D． 中心对称图形和旋转对称图形的区别是什么呢？
见解析
【解析】【试题分析】注意从定义上区别.
【试题解析】中心对称是把一个图形绕其几何中心旋转180度后能够和原来的图形互相重合的图形叫中心对称图形.这个点就是它的对称中心．例如菱形；旋转对称不是旋转一定的角度，而是旋转非周角的角度。就是说不能是旋转360度的整数倍后与自身重合了。例如电扇的叶片转动120°与自身重合，当然菱形也是旋转对称，但并不是所有的旋转对称都是中心对称.
...