题目内容
将点A(1，－3)沿x轴向左平移3个单位长度，再沿y轴向上平移5个单位长度后得到的点A′的坐标为____．
(－2，2)．
【解析】∵点A（1，﹣3）沿x轴向左平移3个单位长度，再沿y轴向上平移5个单位长度后得到点A′，∴点A′的横坐标为1﹣3=﹣2，纵坐标为﹣3+5=2，∴A′的坐标为（﹣2，2）．故答案为：（﹣2，2）．
中心对称图形和旋转对称图形的区别是什么呢？
见解析
【解析】【试题分析】注意从定义上区别.
【试题解析】中心对称是把一个图形绕其几何中心旋转180度后能够和原来的图形互相重合的图形叫中心对称图形.这个点就是它的对称中心．例如菱形；旋转对称不是旋转一定的角度，而是旋转非周角的角度。就是说不能是旋转360度的整数倍后与自身重合了。例如电扇的叶片转动120°与自身重合，当然菱形也是旋转对称，但并不是所有的旋转对称都是中心对称.
... 下列多项式中，不能用完全平方公式分解因式的是（ ）
A.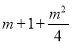 
B. 
C. 
D. 
C
【解析】m+1+=（m2+4m+4）=（m+2）2；-x2+2xy-y2=-（x2-2xy+y2）=-（x-y）2；-a2+14ab+49b2=-（a2-14ab-49b2），它不能用完全平方公式分解因式； -n+1=（n2-6n+9）=（n-3）2，
故选C． 将△ABC各顶点的纵坐标加“﹣3”，连接这三点所成的三角形是由△ABC（ ）
A. 向上平移3个单位得到的 B. 向下平移3个单位得到的
C. 向左平移3个单位得到的 D. 向右平移3个单位得到的
B
【解析】【解析】
△ABC各顶点的纵坐标加“﹣3”，则△ABC向下平移3个单位。故选B． 四边形ABCD各顶点的坐标分别为A(2,4)、B(0,2)、C(2,1)、D(3,2)，将四边形向左平移4个单位长度，再向上平移3个单位长度，得到四边形A′B′C′D′.
(1)四边形A′B′C′D′与四边形ABCD对应点的横坐标有什么关系？纵坐标呢？分别写出A′B′C′D′的坐标；
(2)如果将四边形A′B′C′D′看成是由四边形ABCD经过一次平移得到的，请指出这一平移的方向和距离．
见解析.
【解析】试题分析: (1)根据图形,分别写出四边形A′B′C′D′与四边形ABCD各顶点坐标,对比发现:对应点的横坐标分别减了4,纵坐标分别加了3,A′(－2,7),B′(－4,5),C′(－2,4),D′(－1,5),
(2)连接AA′,根据勾股定理算出:AA′＝＝5.如果将四边形A′B′C′D′看成是由四边形ABCD经过一次平移得到的,那么平移的方向是由A到A′的方向,平... 已知抛物线y= -x2+mx+（7-2m）（m为常数）．
（1）证明：不论m为何值，抛物线与x轴恒有两个不同的交点；
（2）若抛物线与x轴的交点A（x1，0）、B（x2，0）的距离为AB=4（A在B的左边），且抛物线交y轴的正半轴于C，求抛物线的解析式．
（1）证明见解析；（2）抛物线的解析式为y= -x2+2x+3．
【解析】试题分析：（1）要证明抛物线与x轴恒有两个不同的交点证明抛物线的判别式是正数，所以证明判别式是正数即可解决问题；
（2）首先由AB=4可以得|x2-x1|=4，而（x2-x1）2=（x2-x1）2-4x1x2=16，然后利用根与系数的关系即可得到关于m方程，解方程即可求出m，也就求出了抛物线的解析式．
试题... 如图，二次函数y=x2-6x+n的部分图象如图所示，若关于x的一元二次方程x2-6x+n=0的一个解为x1=1，则另一个解x2= ___________.
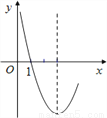
5．
【解析】试题分析：根据二次函数的图象与x轴的交点关于对称轴对称，直接求出x2的值．
试题解析：由图象知，对称轴为x=-
根据二次函数的图象的对称性，
解得：x2=5． 如图，已知二次函数y＝ax2＋bx＋c的部分图象，由图象可知关于x的一元二次方程ax2＋bx＋c＝0的两个根分别是x1＝1.6，x2＝( )
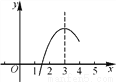
A. －1.6 B. 3.2 C. 4.4 D. 以上都不对
C
【解析】根据图象知道抛物线的对称轴为x=3，根据抛物线是轴对称图象和已知条件即可求出x2．
【解析】
由抛物线图象可知其对称轴为x=3，
又抛物线是轴对称图象，
∴抛物线与x轴的两个交点关于x=3对称，
而关于x的一元二次方程ax2+bx+c=0的两个根分别是x1，x2，
那么两根满足2×3=x1+x2，
而x1=1.6，
∴x2=4.4．
... 等腰三角形是轴对称图形，它的对称轴是( )
A. 过顶点的直线 B. 底边上的高
C. 顶角的平分线所在的直线 D. 腰上的高所在的直线
C
【解析】等腰三角形的对称轴为顶角平分线所在的直线，
故选C．