题目内容
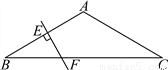
如图，在△ABC中，AB＝AC，∠BAC＝120°，AB的垂直平分线交AB于点E，交BC于点F.若BF＝3cm.求BC.
9cm
【解析】试题分析：先根据等腰三角形性质和三角形内角和定理求出∠B=∠C=30°，根据线段垂直平分线性质和等腰三角形性质求出∠BAF=30°，根据含30度角的直角三角形性质求出AF、FC即可．
试题解析：
∵在△ABC中，AB=AC，∠A=120°，
∴∠B=∠C=30°，
∵AB的垂直平分线EF，
∴AF=BF，
∴∠BAF=∠B=30°，
又∵BF=3...
练习册系列答案
相关题目
下列说法正确的是( )
A. “任意画一个三角形,其内角和为360°”是随机事件
B. 已知某篮球运动员投篮投中的概率为0.6,则他投10次可投中6次
C. 抽样调查选取样本时,所选样本可按自己的喜好选取
D. 检测某城市的空气质量,采用抽样调查法
D
【解析】试题解析：A、“任意画一个三角形，其内角和为360°”是不可能事件，故A错误；
B、已知某篮球运动员投篮投中的概率为0.6，则他投十次可能投中6次，故B错误；
C、抽样调查选取样本时，所选样本要具有广泛性、代表性，故C错误；
D、检测某城市的空气质量，采用抽样调查法，故D正确；
故选：D． 同时掷两枚质地均匀的正方体骰子，骰子的六个面上分别刻有1到6的点数，下列事件中是不可能发生的事件是( )
A. 点数之和为12 B. 点数之和小于3 C. 点数之和大于4且小于8 D. 点数之和为13
D
【解析】试题分析：找到一定不会发生的事件即可．
【解析】
A、6点+6点=12点，为随机事件，不符合题意；
B、例如：1点+1点=2点，为随机事件，不符合题意；
C、例如：1点+5点=6点，为随机事件，不符合题意；
D、两枚骰子点数最大之和为12点，不可能是13点，为不可能事件，符合题意．
故选：D． 已知：如图，四边形ABCD是平行四边形，延长BA至点E，使AE+CD=AD．连结CE，求证：CE平分∠BCD．
证明见解析．
【解析】试题分析：由平行四边形的性质得出AB∥CD，AB=CD，AD=BC，由平行线的性质得出∠E=∠DCE，由已知条件得出BE=BC，由等腰三角形的性质得出∠E=∠BCE，得出∠DCE=∠BCE即可．
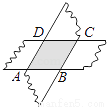
试题解析：∵四边形ABCD是平行四边形，∴AB∥CD，AB=CD，AD=BC，∴∠E=∠DCE，∵AE+CD=AD，∴BE=BC，∴∠E=∠BCE，∴∠DCE=∠BCE，... 如图，剪两张等宽对边平行的纸条，随意交叉叠放在一起，转动其中的一张，重合的部分构成了一个四边形，这个四边形是________．
菱形
【解析】试题分析：首先可判断重叠部分为平行四边形，且两条纸条宽度相同；再由平行四边形的等积转换可得邻边相等，则四边形ABCD为菱形．所以根据菱形的性质进行判断．
【解析】
过点D分别作AB，BC边上的高为AE，AF，
∵四边形ABCD是用两张等宽的纸条交叉重叠地放在一起而组成的图形，
∴AB∥CD，AD∥BC，
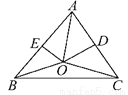
∴四边形ABCD是平行四边形（对边相互平行的四边... 如图，在锐角三角形ABC中，∠BAC＝60°，边AC、AB的垂直平分线交于点O，交AC、AB于点D、E，则∠BOC等于____.
120°
【解析】∵AB,AC的垂直平分线交于点O,
∴OA=OB=OC
∴∠OAB=∠OBA,∠OAC=∠OCA
∴∠OAB+∠OAC=∠OBA+∠OCA=∠A=60°
∴∠OBC+∠OCB=180°-2*60°=60°
∴∠BOC=180°-60°=120°.
故答案是：120°. 中心对称图形和旋转对称图形的区别是什么呢？
见解析
【解析】【试题分析】注意从定义上区别.
【试题解析】中心对称是把一个图形绕其几何中心旋转180度后能够和原来的图形互相重合的图形叫中心对称图形.这个点就是它的对称中心．例如菱形；旋转对称不是旋转一定的角度，而是旋转非周角的角度。就是说不能是旋转360度的整数倍后与自身重合了。例如电扇的叶片转动120°与自身重合，当然菱形也是旋转对称，但并不是所有的旋转对称都是中心对称.
... 如图，不是中心对称图形的是（ ）
A. 
B. 
C. 
D.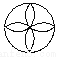 
B
【解析】根据中心对称的定义可以知道B选项不是中心对称图形.故选B. 将△ABC各顶点的纵坐标加“﹣3”，连接这三点所成的三角形是由△ABC（ ）
A. 向上平移3个单位得到的 B. 向下平移3个单位得到的
C. 向左平移3个单位得到的 D. 向右平移3个单位得到的
B
【解析】【解析】
△ABC各顶点的纵坐标加“﹣3”，则△ABC向下平移3个单位。故选B．