题目内容
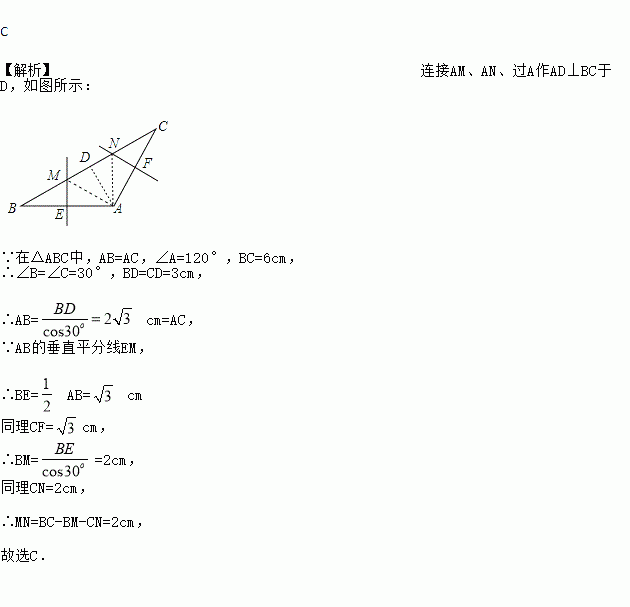
如图，在△ABC中，AB＝AC，∠A＝120°，BC＝6cm，AB的垂直平分线交BC于点M，交AB于点E，AC的垂直平分线交BC于点N，交AC于点F，则MN的长为( )
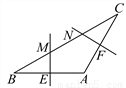
A. 4cm B. 3cm C. 2cm D. 1cm
C
【解析】连接AM、AN、过A作AD⊥BC于D，如图所示：
∵在△ABC中，AB=AC，∠A=120°，BC=6cm，
∴∠B=∠C=30°，BD=CD=3cm，
∴AB= cm=AC，
∵AB的垂直平分线EM，
∴BE= AB= cm
同理CF=cm，
∴BM==2cm，
同理CN=2cm，
∴MN=BC-BM-CN=2cm，
故选C．
练习册系列答案
相关题目
如图，BC=4cm，AB=3cm，AF=12cm，AC⊥AF，正方形CDEF的面积是169cm2，试判断△ABC的形状？
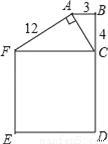
△ABC是直角三角形.
【解析】分析：首先根据正方形的面积求出FC的长，再在Rt△ACF中利用勾股定理求出AC的长，然后根据勾股定理逆定理证明∠B=90°即可．
本题解析：
∵正方形CDEF的面积是169 cm2，
∴FC=13 cm
在Rt△ACF中，由勾股定理得，
AC2=CF2﹣AF2=132﹣122=25，
在△ABC中，因为AB2+BC2=32+... 一个口袋里有5个红球，3个黄球，2个绿球，任意摸一个，摸（ ）的可能性最小.
A. 红球 B. 黄球 C. 绿球 D. 以上都不对
C
【解析】由题意知这个口袋中装有5个红球，3个黄球，2个绿球，共有5+3+2=10个球，摸到红球的概率是，摸到黄球的概率是，摸到绿球的概率是，因此，摸到绿球的可能性最小.
故选C. 如图，剪两张等宽对边平行的纸条，随意交叉叠放在一起，转动其中的一张，重合的部分构成了一个四边形，这个四边形是________．
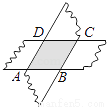
菱形
【解析】试题分析：首先可判断重叠部分为平行四边形，且两条纸条宽度相同；再由平行四边形的等积转换可得邻边相等，则四边形ABCD为菱形．所以根据菱形的性质进行判断．
【解析】
过点D分别作AB，BC边上的高为AE，AF，
∵四边形ABCD是用两张等宽的纸条交叉重叠地放在一起而组成的图形，
∴AB∥CD，AD∥BC，
∴四边形ABCD是平行四边形（对边相互平行的四边... 如图，点D在BC上，DE⊥AB，DF⊥AC，垂足分别为E、F，DE＝DF.求证：AD垂直平分EF.
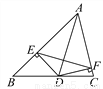
见解析
【解析】试题分析：根据直角三角形的判定定理证明Rt△AED≌Rt△AFD，得到AE=AF，根据线段垂直平分线的判定定理证明结论．
试题解析：
在Rt△AED和Rt△AFD中，
∴Rt△AED≌Rt△AFD（HL），
∴AE=AF，
又∵DE=DF，
∴AD是EF的垂直平分线，即AD垂直平分EF． 中心对称图形和旋转对称图形的区别是什么呢？
见解析
【解析】【试题分析】注意从定义上区别.
【试题解析】中心对称是把一个图形绕其几何中心旋转180度后能够和原来的图形互相重合的图形叫中心对称图形.这个点就是它的对称中心．例如菱形；旋转对称不是旋转一定的角度，而是旋转非周角的角度。就是说不能是旋转360度的整数倍后与自身重合了。例如电扇的叶片转动120°与自身重合，当然菱形也是旋转对称，但并不是所有的旋转对称都是中心对称.
... 关于点O成中心对称的两个四边形ABCD和DEFG，AD、BE、CF、DG都过______
点O
【解析】对应点的连线经过对称中心.
故答案：点O. 分解因式：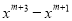 
=____________________.
xm+1(x+1)(x-1)
【解析】= xm+1(x2-1)= xm+1(x+1)(x-1)，
故答案为：xm+1(x+1)(x-1). 四边形ABCD各顶点的坐标分别为A(2,4)、B(0,2)、C(2,1)、D(3,2)，将四边形向左平移4个单位长度，再向上平移3个单位长度，得到四边形A′B′C′D′.
(1)四边形A′B′C′D′与四边形ABCD对应点的横坐标有什么关系？纵坐标呢？分别写出A′B′C′D′的坐标；
(2)如果将四边形A′B′C′D′看成是由四边形ABCD经过一次平移得到的，请指出这一平移的方向和距离．
见解析.
【解析】试题分析: (1)根据图形,分别写出四边形A′B′C′D′与四边形ABCD各顶点坐标,对比发现:对应点的横坐标分别减了4,纵坐标分别加了3,A′(－2,7),B′(－4,5),C′(－2,4),D′(－1,5),
(2)连接AA′,根据勾股定理算出:AA′＝＝5.如果将四边形A′B′C′D′看成是由四边形ABCD经过一次平移得到的,那么平移的方向是由A到A′的方向,平...