题目内容
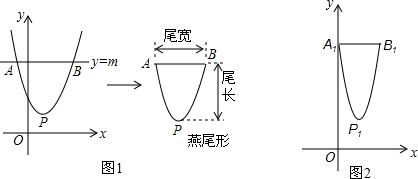
7.如图,抛物线y=a(x-h)2+k(a>0)的顶点为P,直线y=m与x轴平行且与抛物线交于A、B两点,把线段AB与抛物线含顶点部分组成的图形ABP,称作“燕尾形”,顶点P到线段AB的距离称作“尾长”,AB长称作“尾宽”.(1)当“尾长”为8时:
①若a=2,h=k=0,抛物线y=2x2对应的“尾宽”为4;
②若a=2,h=0,k=-8,抛物线y=2x2-8对应的“尾宽”为4;
③若a=2,h=0,k=3,抛物线y=2(x-2)2+3对应的“尾宽”为4;
(2)当“尾长”与“尾宽”相等时:
①若h=k=0,抛物线y=ax2对应的“尾宽”为$\frac{4}{a}$(用含a的式子表示);
②若h=2,k=3,抛物线y=a(x-2)2+3对应的“尾宽”为$\frac{4}{a}$(用含a的式子表示);
③若抛物线y=ax2-4ax+c(a>0)对应的“尾宽”为6,求a的值.
(3)我们把问题(1)③中抛物线y=2(x-2)2+3对应的燕尾形,记为“燕尾1”,相应点记为A1、B1、P1,它在坐标系中的位置如图2所示,把问题(2)③中抛物线y=ax2-4ax+c(c>0)对应的燕尾形,记为“燕尾2”,相应点记为:A2、B2、P2.
试探索:随着字母c的取值变化,“燕尾1”的边界与“燕尾2”的边界存在公共点的个数情况(直接写出探索结果即可).
分析 (1)将尾长等于8时,y对应的值代入解析式,求得x1,x2的值,然后计算出尾宽即可;
(2)设尾长为m,则尾宽为m,将尾宽为m时,y对应的值代入解析式,求得x1,x2的值,然后计算出尾宽,最后根据尾宽$\frac{4}{a}=6$即可求得a的值;
(3)将a=$\frac{2}{3}$代入抛物线y=ax2-4ax+c的解析式得:y=$\frac{2}{3}{x}^{2}-\frac{8}{3}x+c$=$\frac{2}{3}(x-2)^{2}+c-\frac{8}{3}$,其对称轴为x=2,顶点坐标为(2,c-$\frac{8}{3}$),燕尾1的对称轴为x=2,顶点坐标为(2,3),然后对燕尾2进行平移,根据图形找出燕尾2的顶点满足的条件列出等式或不等式,从而可探究出C取值与“燕尾1”的边界与“燕尾2”的边界存在公共点的个数的关系.
解答 解:(1)①当“尾长”为8时,抛物线y=2x2的y=8,将y=8代入抛物线的解析式得:
2x2=8,解得x1=-2,x2=2,
∴“尾宽”=2-(-2)=4.
②抛物线y=2x2-8的尾长为8时,y=0,
将y=0代入得:2x2-8=0,解得:x1=-2,x2=2,
∴“尾宽”=2-(-2)=4.
③抛物线y=2(x-2)2+3尾长为8时,y=11,
将y=11代入y=2(x-2)2+3得2(x-2)2+3=11,
解得:x1=4,x2=0,
故答案为:①4;②4;③4;
(2)①设尾长为m,则尾宽为m.
将y=m代入y=ax2得ax2=m,
解得:x1=$\sqrt{\frac{m}{a}}$,x2=$-\sqrt{\frac{m}{a}}$,
∴2$\sqrt{\frac{m}{a}}$=m,
解得:m=0(舍去),m=$\frac{4}{a}$
②设尾长为m,则尾宽为m.
将y=m+3代入y=a(x-2)2+3得:a(x-2)2+3=m+3,
解得:x1=2+$\sqrt{\frac{m}{a}}$,x2=2$-\sqrt{\frac{m}{a}}$,
∴2$\sqrt{\frac{m}{a}}$=m,
由①可知:m=$\frac{4}{a}$
③由①、②可知$\frac{4}{a}$=6,解得a=$\frac{2}{3}$.
故答案为:①$\frac{4}{a}$;②$\frac{4}{a}$;③$\frac{2}{3}$;
(3)将a=$\frac{2}{3}$代入抛物线y=ax2-4ax+c的解析式得:y=$\frac{2}{3}{x}^{2}-\frac{8}{3}x+c$=$\frac{2}{3}(x-2)^{2}+c-\frac{8}{3}$,其对称轴为x=2,顶点坐标为(2,c-$\frac{8}{3}$),
燕尾1的对称轴为x=2,顶点坐标为(2,3).
如图1,当c-$\frac{8}{3}$<-3时,即c<$-\frac{1}{3}$时,燕尾1与燕尾2的边界不存在交点;
如图2,当c-$\frac{8}{3}$=-3时,即c=$-\frac{1}{3}$时,燕尾1与燕尾2的边界有1个交点;
如图3,当-3<c-$\frac{8}{3}$<3时,即$-\frac{1}{3}$<c<$\frac{17}{3}$时,燕尾1与燕尾2的边界有2个交点;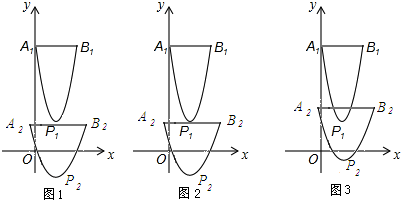
如图4,当c-$\frac{8}{3}$=3时,即c=$\frac{17}{3}$,燕尾1与燕尾2的边界有3个交点;
如图5,当3<c-$\frac{8}{3}$<5时,即:$\frac{17}{3}$<c<$\frac{23}{3}$时,燕尾1与燕尾2的边界有4个交点;
如图6,当c-$\frac{8}{3}$=5时,即c=$\frac{23}{3}$时,燕尾1与燕尾2的边界有无数个交点;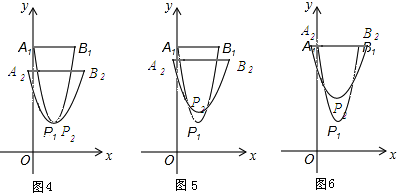
如图7,当5<c-$\frac{8}{3}$<11时,即:$\frac{23}{3}$<c<$\frac{41}{3}$时,燕尾1与燕尾2的边界有2个交点;
如图8,当c-$\frac{8}{3}$=11时,即:c=$\frac{41}{3}$时,燕尾1与燕尾2的边界有1个交点;
如图9,当c-$\frac{8}{3}$>11时,即:c>$\frac{41}{3}$时,燕尾1与燕尾2的边界没有交点.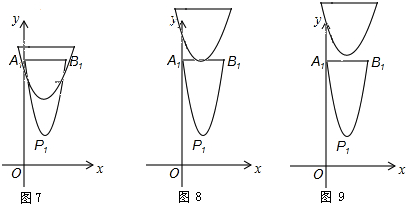
综上所述,当c<$-\frac{1}{3}$或c>$\frac{41}{3}$时,燕尾1与燕尾2的边界没有交点;
当c=$-\frac{1}{3}$或c=$\frac{41}{3}$时,燕尾1与燕尾2的边界有1个交点;
当$-\frac{1}{3}$<c<$\frac{17}{3}$或$\frac{23}{3}$<c<$\frac{41}{3}$时,燕尾1与燕尾2的边界有2个交点;
当c=$\frac{17}{3}$时,燕尾1与燕尾2的边界有3个交点;
当$\frac{17}{3}$<c<$\frac{23}{3}$时,燕尾1与燕尾2的边界有4个交点;
当c=$\frac{23}{3}$时,燕尾1与燕尾2的边界有无数个交点.
点评 本题主要考查的是二次函数的综合应用,解答本题需要同学们读懂题意明确尾宽和尾长的定义,根据题意画出图形,结合图形找出燕尾2顶点的纵坐标的大小与交点个数的关系是解题的关键.

 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案| A. | 6.9m | B. | 7.0m | C. | 7.1m | D. | 6.8m |
| A. | x≠1 | B. | x≠0 | C. | x>1 | D. | x<1 |
| A. | 3 | B. | 4 | C. | 5 | D. | 5或$\sqrt{7}$ |
| A. | 如果直线a,b,c满足a∥b,b∥c,那么a∥c | |
| B. | 三角形的内角和为180° | |
| C. | 内错角相等 | |
| D. | 对顶角相等 |