题目内容
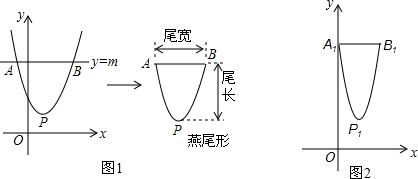
18.已知:矩形ABCD中,M为BC边上一点,AB=10,BC=24,∠BAM=45°,如图1,正方形EFGH的顶点E和点B重合,点F、G、H分别在边AB、AM、BC上.如图2,P为对角线AC上一动点,正方形EFGH从图1的位置出发,以每秒1个单位的速度沿BC向点C匀速移动;同时点P从C点出发,以每秒1个单位的速度沿CA向点A匀速移动.当点F到达线段AC上时,正方形EFGH和点P同时停止运动.设运动时间为t秒,解答下列问题:(1)在整个运动过程中,当点F落在线段AM上和点G落在线段AC上时,分别求出对应t的值;
(2)在整个运动过程中,设正方形EFGH与△AMC重叠部分的面积为S,请直接写出S与t之间的函数关系式以及自变量t的取值范围;
(3)在整个运动过程中,是否存在点P,使△DPG是以DG为腰的等腰三角形?若存在,求出t的值;若不存在,说明理由.
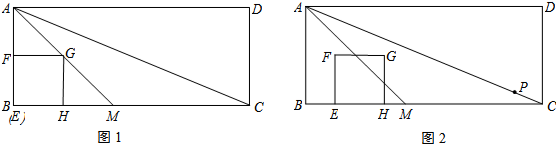
分析 (1)根据正方形的性质和等腰直角三角形的性质可得FG=5,再根据时间=路程÷速度,列出算式求出点F落在线段AM上时t的值;根据三角形中位线的性质以及线段的和差关系得到$\frac{1}{2}$MC=7,再根据时间=路程÷速度,列出算式求出点G落在线段AC上时t的值;
(2)分四种情况:①当0<t≤5时;②当5<t≤7时;③当7<t≤10时;④当10<t≤12时;进行讨论可得S与t之间的函数关系式以及自变量t的取值范围;
(3)先根据勾股定理得到DG2=t2-38t+386,DP2=t2-$\frac{100}{13}$t+100,PG2=$\frac{650}{169}$t2-$\frac{1000}{13}$t+386.再分两种情况:①当DG=DP时,△DPG为等腰三角形;②当DG=PG时,△DPG为等腰三角形;进行讨论列出方程可得t的值.
解答 解:(1)∵AB=10,∠BAM=45°,四边形EFGH为正方形,
∴BM=10,∠FAG=∠FGA=45°,
∴AF=FG=EF=$\frac{1}{2}$AB=5,
∴F为AB的中点,G为AM的中点,
∴t=5÷1=5秒,
又∵当G落在AC上时,所走路程为△AMC的中位线的长.
又∵MC=14,
∴$\frac{1}{2}$MC=7,
∴t=7÷1=7秒;
(2)如图所示: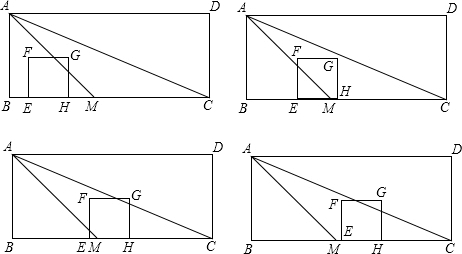
①当0<t≤5时,S=$\frac{1}{2}$t2;
②当5<t≤7时,S=52-$\frac{1}{2}$(10-t)2=-$\frac{1}{2}$t2+10t-25;
③当7<t≤10时,S=52-$\frac{1}{2}$(10-t)2-$\frac{1}{2}$×$\frac{5}{12}$(t-7)2=-$\frac{17}{24}$t2+$\frac{155}{12}$t-$\frac{845}{24}$;
④当10<t≤12时,S=52-$\frac{1}{2}$×$\frac{5}{12}$(t-7)2=-$\frac{5}{24}$t2+$\frac{35}{12}$t+$\frac{355}{24}$;
(3)如图: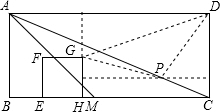
∵DG2=(24-5-t)2+52=t2-38t+386,
DP2=(10-$\frac{5}{13}$t)2+($\frac{12}{13}$t)2=t2-$\frac{100}{13}$t+100,
PG2=(5-$\frac{5}{13}$t)2+(19-$\frac{25}{13}$t)2=$\frac{650}{169}$t2-$\frac{1000}{13}$t+386.
①当DG=DP时,△DPG为等腰三角形,
∴t2-38t+386=t2-$\frac{100}{13}$t+100,
解得t=$\frac{1859}{197}$,
∵$\frac{1859}{197}$<12,
∴存在点P,使△DPG为等腰三角形
②当DG=PG时,△DPG为等腰三角形,
∴t2-38t+386=$\frac{650}{169}$t2-$\frac{1000}{13}$t+386,
∴$\frac{481}{169}$t2-$\frac{506}{13}$t=0,
解得t1=0(舍去),t2=$\frac{506}{37}$>12(舍去).
综上,存在点P,当t=$\frac{1859}{197}$秒时,△DPG是以DG为腰的等腰三角形.
点评 考查了四边形综合题,涉及的知识点有:正方形的性质,等腰直角三角形的性质,时间=路程÷速度,勾股定理,函数思想,方程思想,以及分类思想的运用,综合性较强,有一定的难度.

 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案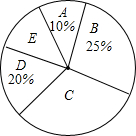 近年来,中学生的身体素质普遍下降,某校为了提高本校学生的身体素质,落实教育部门“在校学生每天体育锻炼时间不少于1小时”的文件精神,对部分学生的每天体育锻炼时间进行了调查统计,以下是本次调查结果的统计表和统计图.
近年来,中学生的身体素质普遍下降,某校为了提高本校学生的身体素质,落实教育部门“在校学生每天体育锻炼时间不少于1小时”的文件精神,对部分学生的每天体育锻炼时间进行了调查统计,以下是本次调查结果的统计表和统计图.| 组别 | A | B | C | D | E |
| 锻炼时间t(分钟) | t<40 | 40≤t<60 | 60≤t<80 | 80≤t<100 | t≥100 |
| 人数 | 12 | 30 | a | 24 | 12 |
(2)统计表中a的值为42;
(3)扇形统计图中C组所在扇形圆心角为126度;
(4)根据调查结果,请你估计该校1200名学生每天体育锻炼时间不少于1小时的学生人数.
(1)求此函数解析式及对称轴;
(2)在对称轴上是否存在一点P,使得△PAB中PA=PB?若存在,求出P的坐标;若不存在,说明理由.
| A. | 8 | B. | 7 | C. | 6 | D. | 5 |
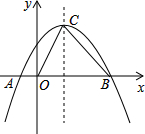 如图,二次函数y=ax2+bx+c图象的顶点坐标为(2,3),与x轴交于点A(-1,0).
如图,二次函数y=ax2+bx+c图象的顶点坐标为(2,3),与x轴交于点A(-1,0).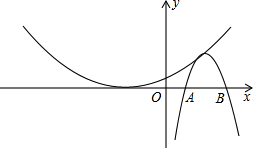 定义:我们把二次函数y=ax2+bx+c和y=-ax2+bx-c这两个二次函数称为一对友好函数,并称函数y=ax2+bx+c是函数y=-ax2+bx-c的友好函数.函数y=-ax2+bx-c也是函数y=ax2+bx+c的友好函数.
定义:我们把二次函数y=ax2+bx+c和y=-ax2+bx-c这两个二次函数称为一对友好函数,并称函数y=ax2+bx+c是函数y=-ax2+bx-c的友好函数.函数y=-ax2+bx-c也是函数y=ax2+bx+c的友好函数.