题目内容
2.某工厂的大门是抛物线型水泥建筑物,大门地面宽为8m,两侧距地面3m处各有一个壁灯,两壁灯之间的水平距离为6m,则大门的高约为( )| A. | 6.9m | B. | 7.0m | C. | 7.1m | D. | 6.8m |
分析 由题意可知,以地面为x轴,大门左边与地面的交点为原点建立平面直角坐标系,抛物线过(0,0)、(8,0)、(1、3)、(7、3),运用待定系数法求出解析式后,求函数的最大值即可.
解答 解:以地面为x轴,大门左边与地面的交点为原点建立平面直角坐标系,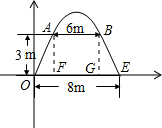
则抛物线过O(0,0)、E(8,0)、A(1、4)、B(7、4)四点,
设该抛物线解析式为:y=ax2+bx+c,
则$\left\{\begin{array}{l}{c=0}\\{64a+8b+c=0}\\{a+b+c=3}\end{array}\right.$,
解得:a=-$\frac{3}{7}$,b=$\frac{24}{7}$.
故函数解析式为:y=-$\frac{3}{7}$x2+$\frac{24}{7}$x.
当x=4时,可得y=-$\frac{48}{7}$+$\frac{96}{7}$=$\frac{48}{7}$≈6.9米.
故厂门的高度约为6.9米.
点评 本题考查点的坐标的求法及二次函数的实际应用关键是建立数学模型,借助二次函数解决实际问题,注意根据线段长度得出各点的坐标.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
13.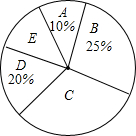 近年来,中学生的身体素质普遍下降,某校为了提高本校学生的身体素质,落实教育部门“在校学生每天体育锻炼时间不少于1小时”的文件精神,对部分学生的每天体育锻炼时间进行了调查统计,以下是本次调查结果的统计表和统计图.
近年来,中学生的身体素质普遍下降,某校为了提高本校学生的身体素质,落实教育部门“在校学生每天体育锻炼时间不少于1小时”的文件精神,对部分学生的每天体育锻炼时间进行了调查统计,以下是本次调查结果的统计表和统计图.
(1)本次被调查的学生数为120人;
(2)统计表中a的值为42;
(3)扇形统计图中C组所在扇形圆心角为126度;
(4)根据调查结果,请你估计该校1200名学生每天体育锻炼时间不少于1小时的学生人数.
 近年来,中学生的身体素质普遍下降,某校为了提高本校学生的身体素质,落实教育部门“在校学生每天体育锻炼时间不少于1小时”的文件精神,对部分学生的每天体育锻炼时间进行了调查统计,以下是本次调查结果的统计表和统计图.
近年来,中学生的身体素质普遍下降,某校为了提高本校学生的身体素质,落实教育部门“在校学生每天体育锻炼时间不少于1小时”的文件精神,对部分学生的每天体育锻炼时间进行了调查统计,以下是本次调查结果的统计表和统计图.| 组别 | A | B | C | D | E |
| 锻炼时间t(分钟) | t<40 | 40≤t<60 | 60≤t<80 | 80≤t<100 | t≥100 |
| 人数 | 12 | 30 | a | 24 | 12 |
(2)统计表中a的值为42;
(3)扇形统计图中C组所在扇形圆心角为126度;
(4)根据调查结果,请你估计该校1200名学生每天体育锻炼时间不少于1小时的学生人数.
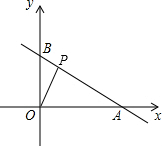 直线y=kx+6与x轴、y轴分别交于A、B两点,点A的坐标为(8,0).
直线y=kx+6与x轴、y轴分别交于A、B两点,点A的坐标为(8,0).