题目内容
阅读下列解题过程:
=
=
-1,
=
=
-
,
请回答下面的问题:
(1)观察上面的解题过程,请直接写出
的值;
(2)利用上面的规律计算:(
+
+
+…+
+
)×(1+
).
| 1 | ||
|
1×(
| ||||
(
|
| 2 |
| 1 | ||||
|
1×(
| ||||||||
(
|
| 3 |
| 2 |
请回答下面的问题:
(1)观察上面的解题过程,请直接写出
| 1 | ||||
|
(2)利用上面的规律计算:(
| 1 | ||
|
| 1 | ||||
|
| 1 | ||||
|
| 1 | ||||
|
| 1 | ||||
|
| 2014 |
考点:分母有理化
专题:规律型
分析:(1)根据观察,可得规律
=
-
;
(2)根据规律,可简便运算.
| 1 | ||||
|
| n |
| n-1 |
(2)根据规律,可简便运算.
解答:解:(1)
=
-
;
(2)原式=(
-1+
-
+
-
+…+
-
+
-
)×(1+
)
=(
-1)(
+1)
=2014-1
=2013.
| 1 | ||||
|
| n |
| n-1 |
(2)原式=(
| 2 |
| 3 |
| 2 |
| 4 |
| 3 |
| 2013 |
| 2012 |
| 2014 |
| 2013 |
| 2014 |
=(
| 2014 |
| 2014 |
=2014-1
=2013.
点评:本题考查了分母有理化,利用了平方差公式进行分母有理化.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 给出如图.
给出如图.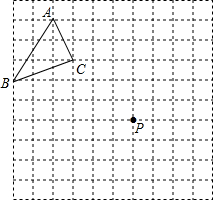 如图,在网格中有△ABC,将点A平移到点P,画出△ABC平移后的图形.
如图,在网格中有△ABC,将点A平移到点P,画出△ABC平移后的图形. 如图,根据函数y=kx+b(k,b是常数,且k≠0)的图象,求:
如图,根据函数y=kx+b(k,b是常数,且k≠0)的图象,求:
