题目内容
 定义:如果一个y与x的函数图象经过平移后能与某反比例函数的图象重合,那么称这个函数是y与x的“反比例平移函数”.
定义:如果一个y与x的函数图象经过平移后能与某反比例函数的图象重合,那么称这个函数是y与x的“反比例平移函数”.例如:y=
| 1 |
| x-2 |
| 1 |
| x |
| 1 |
| x-2 |
(1)若矩形的两边分别是2cm、3cm,当这两边分别增加x(cm)、y(cm)后,得到的新矩形的面积为8cm2,求y与x的函数表达式,并判断这个函数是否为“反比例平移函数”.
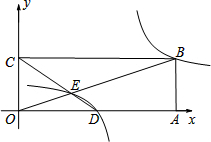
(2)如图,在平面直角坐标系中,点O为原点,矩形OABC的顶点A、C的坐标分别为(9,0)、(0,3).点D是OA的中点,连接OB、CD交于点E,“反比例平移函数”y=
| ax+k |
| x-6 |
(3)在(2)的条件下,已知过线段BE中点的一条直线l交这个“反比例平移函数”图象于P、Q两点(P在Q的右侧),若B、E、P、Q为顶点组成的四边形面积为16,请求出点P的坐标.
考点:反比例函数综合题
专题:
分析:(1)根据新矩形的面积为8cm2,则长乘以宽等于面积,即可得到一个关于x,y的方程,即可变形成函数的形式,进行判断;
(2)把B和D的坐标代入y=
即可列方程求得a、k的值,则函数解析式即可求解;
(3)由反比例函数的中心对称性,四边形PEQB为平行四边形,设P1(x0,y0),根据S△OP1E=S四边形ONMC-S△OCP1-S△MP1E-S△ONE.即可列方程求解.
(2)把B和D的坐标代入y=
| ax+k |
| x-6 |
(3)由反比例函数的中心对称性,四边形PEQB为平行四边形,设P1(x0,y0),根据S△OP1E=S四边形ONMC-S△OCP1-S△MP1E-S△ONE.即可列方程求解.
解答: 解:(1)(x+2)(y+3)=8,
解:(1)(x+2)(y+3)=8,
∴y=
-3,向右平移2个单位,再向上平移3个单位得到y=
.
∴y=
-3是“反比例平移函数”.
(2)把B和D的坐标代入y=
得:
,
解得:
,
则“反比例平移函数”的表达式为y=
.
故变换后的反比例函数表达式为y=
.
(3)如图,当点P在点B左侧时,设线段BE的中点为F,由反比
例函数中心对称性,四边形PEQB为平行四边形.
∵四边形PEQB的面积为16,∴S△PFE=4,
∵B(9,3),F(6,2).
y=
是y=
的“反比例平移函数”,
∴S△PFE=S△POE=4,点E的坐标是:(3,1)
过E作x轴的垂线,与BC、x轴分别交于M、N点.
S△OP1E=S四边形ONMC-S△OCP1-S△MP1E-S△ONE.
设P1(x0,y0),
∴
即
∴
∴P1(1,3),
∴点P的坐标为(7,5).
当点P在点B右侧时,同理可得点P的坐标为(15,
).
 解:(1)(x+2)(y+3)=8,
解:(1)(x+2)(y+3)=8,∴y=
| 8 |
| x+2 |
| 8 |
| x |
∴y=
| 8 |
| x+2 |
(2)把B和D的坐标代入y=
| ax+k |
| x-6 |
|
解得:
|
则“反比例平移函数”的表达式为y=
| 2x-9 |
| x-6 |
故变换后的反比例函数表达式为y=
| 3 |
| x |
(3)如图,当点P在点B左侧时,设线段BE的中点为F,由反比
例函数中心对称性,四边形PEQB为平行四边形.
∵四边形PEQB的面积为16,∴S△PFE=4,
∵B(9,3),F(6,2).
y=
| 2x-9 |
| x-6 |
| 3 |
| x |
∴S△PFE=S△POE=4,点E的坐标是:(3,1)
过E作x轴的垂线,与BC、x轴分别交于M、N点.
S△OP1E=S四边形ONMC-S△OCP1-S△MP1E-S△ONE.
设P1(x0,y0),
∴
|
即
|
∴
|
∴P1(1,3),
∴点P的坐标为(7,5).
当点P在点B右侧时,同理可得点P的坐标为(15,
| 7 |
| 3 |
点评:本题考查了反比例函数的性质,以及待定系数法求函数的解析式,注意到本题中的反比例平移函数与反比例函数的关系是关键.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
如图,将边长分别为1、2、3、5、…的若干正方形按一定的规律拼成不同的矩形,依次记作矩形①、矩形②、矩形③、矩形④、…,那么按此规律,矩形⑧的周长应该为( )


| A、288 | B、220 |
| C、178 | D、110 |

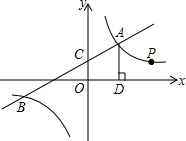 如图,一次函数y1=k1x+2与反比例函数y2=
如图,一次函数y1=k1x+2与反比例函数y2= 已知:如图,AB∥CD,∠A=∠D,试说明AC∥DE成立的理由.
已知:如图,AB∥CD,∠A=∠D,试说明AC∥DE成立的理由. 已知:如图,∠ADC=117°.试求∠A+∠B+∠C的度数.
已知:如图,∠ADC=117°.试求∠A+∠B+∠C的度数.