题目内容
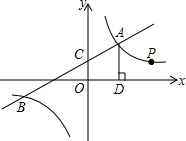 如图,一次函数y1=k1x+2与反比例函数y2=
如图,一次函数y1=k1x+2与反比例函数y2=| k2 |
| x |
(1)求一次函数和反比例函数的表达式.
(2)根据函数图象可知,当y1>y2时,x的值.
(3)过A点作AD⊥x轴于点D,点P是反比例函数在第一象限的图象上一点.设直线OP与线段AD交于点E,且DE=
| 1 |
| 4 |
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)把B的坐标代入两函数的解析式,即可求出答案;
(2)根据图象和A、B的横坐标得出即可;
(3)先求出E的坐标,设出直线OP的解析式,把E的坐标代入求出即可.
(2)根据图象和A、B的横坐标得出即可;
(3)先求出E的坐标,设出直线OP的解析式,把E的坐标代入求出即可.
解答:解:(1)将B(-8,-2)代入y1=k1x+2,可得-2=-8k1+2,
∴k1=
,
∴一次函数的表达式为y1=
x+2;
将B(-8,-2)代入y2=
,
可得-2=
,
∴k2=16,
∴反比例函数的表达式为y2=
;
(2)∵A(4,m)和B(-8,-2),
∴根据函数图象可知,当y1>y2时,x的值是-8<x<0或x>4;

(3)将A(4,m)代入y2=
,
得m=
=4,
∴点A的坐标是(4,4),
∵AD⊥x轴于点D,且AD=4,DE=
AD,
∴E(4,1).
设直线OP的表达式为y=ax,
将E(4,1)代入此式,可得1=4a,
∴a=
,
∴直线OP的表达式为y=
x.
∴k1=
| 1 |
| 2 |
∴一次函数的表达式为y1=
| 1 |
| 2 |
将B(-8,-2)代入y2=
| k2 |
| x |
可得-2=
| k2 |
| -8 |
∴k2=16,
∴反比例函数的表达式为y2=
| 16 |
| x |
(2)∵A(4,m)和B(-8,-2),
∴根据函数图象可知,当y1>y2时,x的值是-8<x<0或x>4;

(3)将A(4,m)代入y2=
| 16 |
| x |
得m=
| 16 |
| 4 |
∴点A的坐标是(4,4),
∵AD⊥x轴于点D,且AD=4,DE=
| 1 |
| 4 |
∴E(4,1).
设直线OP的表达式为y=ax,
将E(4,1)代入此式,可得1=4a,
∴a=
| 1 |
| 4 |
∴直线OP的表达式为y=
| 1 |
| 4 |
点评:本题考查了一次函数和反比例函数的交点问题,用待定系数法求出一次函数和反比例函数的解析式,函数的图象等知识点的应用,主要考查学生的计算能力、观察图象的能力,题目比较好,难度适中.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
下列计算中正确的是( )
| A、(m-n)2=m2-n2 | ||||
| B、(-3p+q)2=3p2-6pq+q2 | ||||
C、(
| ||||
| D、(a+2b)2=a2+2ab+4b2 |
 如图,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1+∠2=90°.求证:
如图,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1+∠2=90°.求证: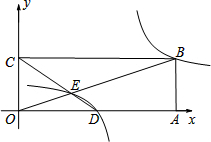 定义:如果一个y与x的函数图象经过平移后能与某反比例函数的图象重合,那么称这个函数是y与x的“反比例平移函数”.
定义:如果一个y与x的函数图象经过平移后能与某反比例函数的图象重合,那么称这个函数是y与x的“反比例平移函数”. 投掷一枚质地均匀的正方体骰子.
投掷一枚质地均匀的正方体骰子.