题目内容
6. 如图,等边△ABC和等边△ADE中,AB=2$\sqrt{7}$,AD=2$\sqrt{3}$,连CE,BE,当∠AEC=150°时,则BE=4.
如图,等边△ABC和等边△ADE中,AB=2$\sqrt{7}$,AD=2$\sqrt{3}$,连CE,BE,当∠AEC=150°时,则BE=4.
分析 如作CM⊥AE于M,设CM=a,在RT△ACM利用勾股定理求出a,再求出CE,由△CAE≌△BAD,得到EC=BD,在RT△EBD中利用勾股定理即可求出BE.
解答 解:如作CM⊥AE于M,设CM=a,
∵△ABC、△ADE都是等边三角形,
∴AC=AB=2$\sqrt{7}$,AE=AD=DE=2$\sqrt{3}$,∠CAB=∠EAD=∠EDA=60°,
∴∠CAE=∠BAD,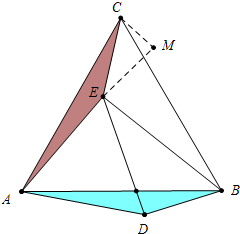
在△CAE和△BAD中,
$\left\{\begin{array}{l}{CA=BA}\\{∠CAE=∠BAD}\\{EA=DA}\end{array}\right.$,
∴△CAE≌△BAD,
∴EC=BD,∴∠AEC=∠ADB=150°,
∴∠EDB=90°,
∵∠AEC=150°,
∴∠CEM=180°-∠AEC=30°,
∴EM=$\sqrt{3}$a,
在RT△ACM中,∵AC2=CM2+AM2,
∴28=a2+(2$\sqrt{3}$+$\sqrt{3}$a)2
a=1(或-4舍弃),
∴EC=BD=2CM=2,
在RT△EBD中,∵DE=2$\sqrt{3}$,BD=2,
∴EB=$\sqrt{D{E}^{2}+D{B}^{2}}$=$\sqrt{(2\sqrt{3})^{2}+{2}^{2}}$=4.
故答案为4.
点评 本题考查全等三角形的判定和性质、等边三角形的性质、直角三角形中30度角的性质,解题的关键是利用150°构造30°的直角三角形,求出相应的线段,属于中考常考题型.

练习册系列答案
相关题目
18.与抛物线y=-2x2的形状相同,顶点是(-1,3)的二次函数解析式为( )
| A. | y=-2(x-1)2+3 | B. | y=±2(x+1)2+3 | C. | y=±2(x-1)2+3 | D. | y=-2(x+1)2+3 |
16.直线l:y=3x经过平移得到直线l2,直线l2经过点(m,n),且m,n满足关系6m-2n=-4,则l2是由l1( )
| A. | 向上平移2个单位长度得到的 | B. | 向上平移4个单位长度得到的 | ||
| C. | 向下平移2个单位长度得到的 | D. | 向下平移4个单位长度得到的 |
 已知:△ABC边AB=m,BC=n,AC边上中线为BD=p,求作△ABC.
已知:△ABC边AB=m,BC=n,AC边上中线为BD=p,求作△ABC. 如图,点D在⊙O的弦AB上移动,AB=6,连接OD,过点D作OD的垂线交⊙O于点C,则CD的最大值是3.
如图,点D在⊙O的弦AB上移动,AB=6,连接OD,过点D作OD的垂线交⊙O于点C,则CD的最大值是3.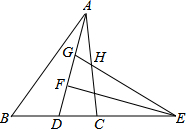 如图,在△ABC中,5AB=6AC,AD为△ABC的角平分线,点E在BC的延长线上,EF⊥AD于点F,点G在AF上,FG=FD,连接EG交AC于点H.若点H是AC的中点,则$\frac{AG}{FD}$的值为$\frac{10}{7}$.
如图,在△ABC中,5AB=6AC,AD为△ABC的角平分线,点E在BC的延长线上,EF⊥AD于点F,点G在AF上,FG=FD,连接EG交AC于点H.若点H是AC的中点,则$\frac{AG}{FD}$的值为$\frac{10}{7}$.