题目内容
18.(1)已知:(x+y)2+|3-y|=0,求$\frac{x-y}{xy}$的值;(2)当式子3-(x+y)2有最大值时,最大值是3;此时x与y的关系为互为相反数.
分析 (1)根据非负数的性质列出方程求出x、y的值,代入所求代数式计算即可;
(2)根据偶次方的非负性解答即可.
解答 解:(1)由题意得,x+y=0,3-y=0,
解得,x=-3,y=3
则$\frac{x-y}{xy}$=$\frac{2}{3}$;
(2)∵(x+y)2≥0,
∴-(x+y)2≤0,
∴3-(x+y)2有最大值3,x与y互为相反数,
故答案为:3;互为相反数.
点评 本题考查的是非负数的性质和偶次方的非负性,掌握几个非负数的和为0时,这几个非负数都为0是解题的关键.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
10.据市旅游局统计,今年“十•一”长假期间,我市旅游市场走势良好,假期旅游总收入达到1.5亿元,用科学记数法可以表示为( )
| A. | 1.5×106 | B. | 1.5×107 | C. | 1.5×108 | D. | 1.5×109 |
8.程程家进行装修,程程的爸爸想用某种图形的地砖无间隙地铺设地面,下列的多边形地砖不能用于此次地面的铺设的是( )
| A. | 正三角形 | B. | 正方形 | C. | 正五边形 | D. | 正六边形 |
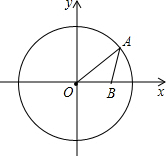 如图,在平面直角坐标系中,O为坐标原点,⊙O的半径为5,点B的坐标为(3,0),点A为⊙O上一动点,当∠OAB取最大值时,点A的坐标为(3,4)或(3,-4).
如图,在平面直角坐标系中,O为坐标原点,⊙O的半径为5,点B的坐标为(3,0),点A为⊙O上一动点,当∠OAB取最大值时,点A的坐标为(3,4)或(3,-4). 如图,等边△ABC和等边△ADE中,AB=2$\sqrt{7}$,AD=2$\sqrt{3}$,连CE,BE,当∠AEC=150°时,则BE=4.
如图,等边△ABC和等边△ADE中,AB=2$\sqrt{7}$,AD=2$\sqrt{3}$,连CE,BE,当∠AEC=150°时,则BE=4. 如图,在等腰△ABC中,AB=BC=4,点O是AB的中点,∠AOC=60°,点P是射线CO上的一个动点,若当△PAB为直角三角线时,试画出可能的图形(两种即可),并求出相应图形中的AP的长.
如图,在等腰△ABC中,AB=BC=4,点O是AB的中点,∠AOC=60°,点P是射线CO上的一个动点,若当△PAB为直角三角线时,试画出可能的图形(两种即可),并求出相应图形中的AP的长. 如图,点A在射线OX上,OA的长等于2cm.如果OA绕点O按逆时针方向旋转30°到OA′,那么点A′的位置可以用(2,30°)表示.如果将OA′再沿逆时针方向继续旋转55°到OA′,那么点A′的位置可以用(2,85°)表示.
如图,点A在射线OX上,OA的长等于2cm.如果OA绕点O按逆时针方向旋转30°到OA′,那么点A′的位置可以用(2,30°)表示.如果将OA′再沿逆时针方向继续旋转55°到OA′,那么点A′的位置可以用(2,85°)表示.