题目内容
14.以线段AC为对角线的四边形ABCD(它的四个顶点A、B、C、D按顺时针方向排列),已知AB=BC=CD,∠ABC=100°,∠CAD=40°;则∠BCD的大小为80°或100°.分析 根据等腰三角形的性质和平行线的判定可得AD∥BC,再分2种情况:(1)如图1,过点C分别作CE⊥AB于E,CF⊥AD于F,通过证明Rt△ACE≌Rt△ACF,Rt△BCE≌Rt△DCF,由全等三角形的性质得到∠2=∠ACD=40°,可得∠BCD=80°;(2)如图2,根据等腰梯形的判定可得四边形ABCD′是等腰梯形,再根据等腰梯形的性质得到∠BCD′=∠ABC=100°,从而求解.
解答 解:∵AB=BC,∠ABC=100°,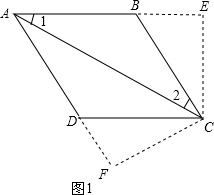 ∴∠1=∠2=∠CAD=40°,
∴∠1=∠2=∠CAD=40°,
∴AD∥BC,
(1)如图1,过点C分别作CE⊥AB于E,CF⊥AD于F,
∵∠1=∠CAD,
∴CE=CF,
在Rt△ACE与Rt△ACF中,
$\left\{\begin{array}{l}{AC=AC}\\{CE=CF}\end{array}\right.$,
∴Rt△ACE≌Rt△ACF,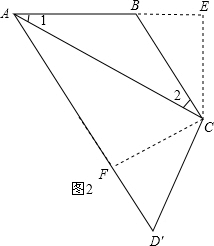 在Rt△BCE与Rt△DCF中,
在Rt△BCE与Rt△DCF中,
$\left\{\begin{array}{l}{CB=CD}\\{CE=CF}\end{array}\right.$,
∴Rt△BCE≌Rt△DCF,
∴∠ACE=∠ACF,∠BCE=∠△DCF,
∴∠2=∠ACD=40°,
∴∠BCD=80°;
(2)如图2,∵AD∥BC,AB=CD′,
∴四边形ABCD′是等腰梯形,
∴∠BCD′=∠ABC=100°.
综上所述,∠BCD=80°或100°.
点评 考查了全等三角形的判定与性质,等腰梯形的判定与性质,本题关键是证明Rt△ACE≌Rt△ACF,Rt△BCE≌Rt△DCF,同时注意分类思想的应用.

练习册系列答案
相关题目
6.已知$\sqrt{15129}$=123,$\sqrt{x}$=0.123,则x=( )
| A. | 0.15129 | B. | 0.015129 | C. | 0.0015129 | D. | 1.5129 |
19. 如图,DC是以AB为直径的半圆上的弦,DM⊥CD交AB于点M,CN⊥CD交AB于点N.AB=10,CD=6.则四边形DMNC的面积( )
如图,DC是以AB为直径的半圆上的弦,DM⊥CD交AB于点M,CN⊥CD交AB于点N.AB=10,CD=6.则四边形DMNC的面积( )
 如图,DC是以AB为直径的半圆上的弦,DM⊥CD交AB于点M,CN⊥CD交AB于点N.AB=10,CD=6.则四边形DMNC的面积( )
如图,DC是以AB为直径的半圆上的弦,DM⊥CD交AB于点M,CN⊥CD交AB于点N.AB=10,CD=6.则四边形DMNC的面积( )| A. | 等于24 | B. | 最小为24 | C. | 等于48 | D. | 最大为48 |
4.下列运算正确的为( )
| A. | (4xy2)2=8x2y4 | B. | 3x2=9x2 | C. | (-x)7÷(-x)2=-x5 | D. | (6xy2)2÷2xy=3xy3 |
 如图,在△ABC中,∠ACB=90°,点O是三角形内的一点,且S△OAB=S△OBC=S△OAC,那么$\frac{O{A}^{2}+O{B}^{2}}{O{C}^{2}}$值为5.
如图,在△ABC中,∠ACB=90°,点O是三角形内的一点,且S△OAB=S△OBC=S△OAC,那么$\frac{O{A}^{2}+O{B}^{2}}{O{C}^{2}}$值为5.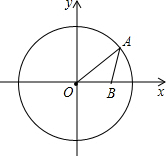 如图,在平面直角坐标系中,O为坐标原点,⊙O的半径为5,点B的坐标为(3,0),点A为⊙O上一动点,当∠OAB取最大值时,点A的坐标为(3,4)或(3,-4).
如图,在平面直角坐标系中,O为坐标原点,⊙O的半径为5,点B的坐标为(3,0),点A为⊙O上一动点,当∠OAB取最大值时,点A的坐标为(3,4)或(3,-4). 如图,等边△ABC和等边△ADE中,AB=2$\sqrt{7}$,AD=2$\sqrt{3}$,连CE,BE,当∠AEC=150°时,则BE=4.
如图,等边△ABC和等边△ADE中,AB=2$\sqrt{7}$,AD=2$\sqrt{3}$,连CE,BE,当∠AEC=150°时,则BE=4. 如图,点A在射线OX上,OA的长等于2cm.如果OA绕点O按逆时针方向旋转30°到OA′,那么点A′的位置可以用(2,30°)表示.如果将OA′再沿逆时针方向继续旋转55°到OA′,那么点A′的位置可以用(2,85°)表示.
如图,点A在射线OX上,OA的长等于2cm.如果OA绕点O按逆时针方向旋转30°到OA′,那么点A′的位置可以用(2,30°)表示.如果将OA′再沿逆时针方向继续旋转55°到OA′,那么点A′的位置可以用(2,85°)表示.