题目内容
15.(1)解方程:$\frac{x}{x-1}-1=\frac{3}{{({x+2})({x-1})}}$;(2)解不等式组:$\left\{\begin{array}{l}2x-1>x+1\\ x+8<4x-1\end{array}\right.$,并把解集在数轴上表示出来.
分析 (1)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解;
(2)分别求出不等式组中两不等式的解集,找出解集的公共部分,表示在数轴上即可.
解答 解:(1)去分母得:x2+2x-x2-x+2=3,
解得:x=1,
经检验x=1是增根,分式方程无解;
(2)$\left\{\begin{array}{l}{2x-1>x+1①}\\{x+8<4x-1②}\end{array}\right.$,
由①得:x>2,
由②得:x>3,
则不等式组的解集为x>3.
点评 此题考查了解分式方程,以及解一元一次不等式组,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
10.据市旅游局统计,今年“十•一”长假期间,我市旅游市场走势良好,假期旅游总收入达到1.5亿元,用科学记数法可以表示为( )
| A. | 1.5×106 | B. | 1.5×107 | C. | 1.5×108 | D. | 1.5×109 |
4.下列运算正确的为( )
| A. | (4xy2)2=8x2y4 | B. | 3x2=9x2 | C. | (-x)7÷(-x)2=-x5 | D. | (6xy2)2÷2xy=3xy3 |
5.下列运算正确的是( )
| A. | a3+a4=a7 | B. | 2a3•a4=2a7 | C. | 2(a4)3=2a7 | D. | a8÷a4=a2 |
 如图,等边△ABC和等边△ADE中,AB=2$\sqrt{7}$,AD=2$\sqrt{3}$,连CE,BE,当∠AEC=150°时,则BE=4.
如图,等边△ABC和等边△ADE中,AB=2$\sqrt{7}$,AD=2$\sqrt{3}$,连CE,BE,当∠AEC=150°时,则BE=4. 如图,点A在射线OX上,OA的长等于2cm.如果OA绕点O按逆时针方向旋转30°到OA′,那么点A′的位置可以用(2,30°)表示.如果将OA′再沿逆时针方向继续旋转55°到OA′,那么点A′的位置可以用(2,85°)表示.
如图,点A在射线OX上,OA的长等于2cm.如果OA绕点O按逆时针方向旋转30°到OA′,那么点A′的位置可以用(2,30°)表示.如果将OA′再沿逆时针方向继续旋转55°到OA′,那么点A′的位置可以用(2,85°)表示.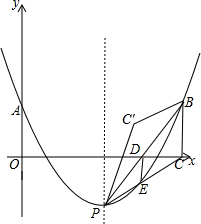 如图,抛物线y=a(x-$\sqrt{2}$m)2-m(其中m>1)与其对称轴l相交于点P,与y轴相交于点A(0,m).点A关于直线l的对称点为B,作BC⊥x轴于点C,连接PC、PB,与抛物线、x轴分别相交于点D、E,连接DE.将△PBC沿直线PB翻折,得到△PBC′.
如图,抛物线y=a(x-$\sqrt{2}$m)2-m(其中m>1)与其对称轴l相交于点P,与y轴相交于点A(0,m).点A关于直线l的对称点为B,作BC⊥x轴于点C,连接PC、PB,与抛物线、x轴分别相交于点D、E,连接DE.将△PBC沿直线PB翻折,得到△PBC′.