题目内容
圆内接正方形的一边所对的圆周角等于 ．
考点：正多边形和圆
专题：
分析：根据题意画出图形，根据等边三角形性质求出∠A，根据圆内接四边形性质求出∠D，即可得出答案．
解答：解：如图：
∵△ABC是等边三角形，
∴∠A=60°，
∵A、B、D、C四点共圆，
∴∠D+∠A=180°，
∴∠D=120°，
即等边三角形的一边所对的圆周角是60°或120°，
故答案为：60°或120°．
∵△ABC是等边三角形，
∴∠A=60°，
∵A、B、D、C四点共圆，
∴∠D+∠A=180°，
∴∠D=120°，
即等边三角形的一边所对的圆周角是60°或120°，
故答案为：60°或120°．
点评：本题考查了圆内接四边形的性质，等边三角形的性质，解此题的关键是能求出符合条件的所有情况．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
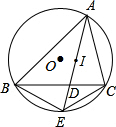如图，△ABC内接于⊙O，I是△ABC的内心，AI交BC于点D，交⊙O于点E，试说明BE、CE、IE的大小关系．
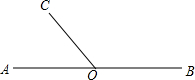如图，点O为直线AB上一点，∠AOC=50°．
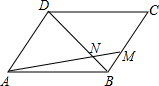如图，在?ABCD中，M是边BC上的一点，AM与BD相交于点N，且AM：NM=4：1．
如图，点B、D、C是⊙A上的点，∠BDC=130°，则∠BAC=
某小区有100个停车位，给业主停车带来了方便，去年1-6月，每个车位租价y为360元，7-12月，每个车位租价y（元）与月份x关系如表所示．去年1-12月，每月租出车位m（个）与月份x关系如图．已知业主只需支付月租给物管公司，公司每月每车位需支付管理费p=6x（1≤x≤12，x取整数）．