题目内容
 如图,点B、D、C是⊙A上的点,∠BDC=130°,则∠BAC=
如图,点B、D、C是⊙A上的点,∠BDC=130°,则∠BAC=考点:圆周角定理
专题:
分析:首先在优弧
上取点E,连接BE,CE,由点B、D、C是⊙A上的点,∠BDC=130°,即可求得∠E的度数,然后由圆周角定理,即可求得答案.
 |
| BC |
解答: 解:在优弧
解:在优弧
上取点E,连接BE,CE,
∵∠BDC=130°,
∴∠E=180°-∠BDC=50°,
∴∠BAC=2∠E=100°.
故答案为:100°.
 解:在优弧
解:在优弧 |
| BC |
∵∠BDC=130°,
∴∠E=180°-∠BDC=50°,
∴∠BAC=2∠E=100°.
故答案为:100°.
点评:此题考查了圆周角定理以及圆的内接四边形的性质.此题难度不大,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
设x3-3
x2+6x-2
-8=0,则x5-41x2+1的值为( )
| 2 |
| 2 |
A、13-
| ||
B、-13+
| ||
| C、-13 | ||
| D、13 |
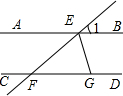 如图,AB∥CD,EF交AB、CD于点E、F、EG平分∠BEF,交CD于点G.若∠1=40°,则∠EGF=( )
如图,AB∥CD,EF交AB、CD于点E、F、EG平分∠BEF,交CD于点G.若∠1=40°,则∠EGF=( )| A、20° | B、40° |
| C、70° | D、110° |
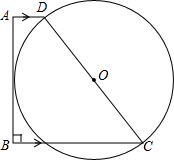 已知,如图,ABCD为直角梯形,AB⊥BC,CD=AD+BC,
已知,如图,ABCD为直角梯形,AB⊥BC,CD=AD+BC,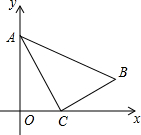 如图,△ABC中,A,B,C三点的坐标分别是A(0,
如图,△ABC中,A,B,C三点的坐标分别是A(0,