题目内容
已知一个正n边形的外接圆半径和内切圆半径分别为20cm和10
cm,求这个多边形的面积.
| 3 |
考点:正多边形和圆
专题:
分析:正n边形的外接圆半径和内切圆半径以及正n边形边长的一半正好组成直角三角形,从而可得出正n边形的边长和中心角,再求面积即可.
解答:解:设正n边形的外接圆半径和内切圆半径以及正n边形边长的一半分别为R,r,a,
则R=20cm,r=10
cm,
∴a2+r2=R2,
解得a=10cm,
∴正n边形边长为20cm,
∴中心角为60°,
∴n=6,
∴S=6×
×2a×r=6ar=6×10×10
=600
cm2.
则R=20cm,r=10
| 3 |
∴a2+r2=R2,
解得a=10cm,
∴正n边形边长为20cm,
∴中心角为60°,
∴n=6,
∴S=6×
| 1 |
| 2 |
| 3 |
| 3 |
点评:本题考查了正多边形和圆,以及勾股定理.此题难度适中,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
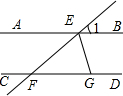 如图,AB∥CD,EF交AB、CD于点E、F、EG平分∠BEF,交CD于点G.若∠1=40°,则∠EGF=( )
如图,AB∥CD,EF交AB、CD于点E、F、EG平分∠BEF,交CD于点G.若∠1=40°,则∠EGF=( )| A、20° | B、40° |
| C、70° | D、110° |
下面的计算正确的是( )
| A、3x2•4x2=12x2 |
| B、(xy5)3=xy15 |
| C、x4÷x=x3 |
| D、(x5)2=x2 |
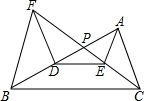 如图,在△ABC中,点D是AB上一点,E是△ABC内一点,DE∥BC,过点D作AC的平行线交CE的延长线于点F,CF与AB交于P,求证:BF∥AE.
如图,在△ABC中,点D是AB上一点,E是△ABC内一点,DE∥BC,过点D作AC的平行线交CE的延长线于点F,CF与AB交于P,求证:BF∥AE.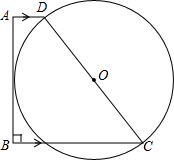 已知,如图,ABCD为直角梯形,AB⊥BC,CD=AD+BC,
已知,如图,ABCD为直角梯形,AB⊥BC,CD=AD+BC,