题目内容
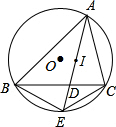 如图,△ABC内接于⊙O,I是△ABC的内心,AI交BC于点D,交⊙O于点E,试说明BE、CE、IE的大小关系.
如图,△ABC内接于⊙O,I是△ABC的内心,AI交BC于点D,交⊙O于点E,试说明BE、CE、IE的大小关系.考点:三角形的内切圆与内心
专题:
分析:如图,作辅助线;首先证明BE=CE;进而证明∠BIE=∠IBE,得到BE=IE,即可解决问题.
解答: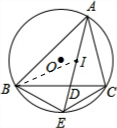 解:BE=IE=CE;理由如下:
解:BE=IE=CE;理由如下:
如图,连接BI;
∵I是△ABC的内心,
∴∠BAE=∠CAE,
∴
=
,
∴BE=CE;
∵I是△ABC的内心,
∴∠BAI=∠CAI(设为α),∠IBC=∠ABI(设为β);
∴∠EBC=∠CAI=α;
∵∠BIE=∠BAI+∠ABI=α+β,而∠IBE=α+β,
∴∠BIE=∠IBE,
∴BE=IE,
∴BE=IE=CE.
 解:BE=IE=CE;理由如下:
解:BE=IE=CE;理由如下:如图,连接BI;
∵I是△ABC的内心,
∴∠BAE=∠CAE,
∴
 |
| BE |
 |
| CE |
∴BE=CE;
∵I是△ABC的内心,
∴∠BAI=∠CAI(设为α),∠IBC=∠ABI(设为β);
∴∠EBC=∠CAI=α;
∵∠BIE=∠BAI+∠ABI=α+β,而∠IBE=α+β,
∴∠BIE=∠IBE,
∴BE=IE,
∴BE=IE=CE.
点评:该题主要考查了三角形内切圆的性质及其应用问题;解题的关键是作辅助线,灵活运用有关定理来判断、解答.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
设x3-3
x2+6x-2
-8=0,则x5-41x2+1的值为( )
| 2 |
| 2 |
A、13-
| ||
B、-13+
| ||
| C、-13 | ||
| D、13 |
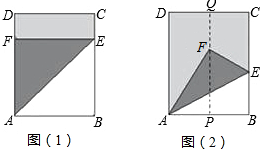 在一张长方形纸片ABCD中,AD=5cm,AB=4cm,现将这张纸片按图示方式折叠,请分别求出折痕的长.
在一张长方形纸片ABCD中,AD=5cm,AB=4cm,现将这张纸片按图示方式折叠,请分别求出折痕的长.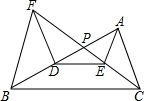 如图,在△ABC中,点D是AB上一点,E是△ABC内一点,DE∥BC,过点D作AC的平行线交CE的延长线于点F,CF与AB交于P,求证:BF∥AE.
如图,在△ABC中,点D是AB上一点,E是△ABC内一点,DE∥BC,过点D作AC的平行线交CE的延长线于点F,CF与AB交于P,求证:BF∥AE.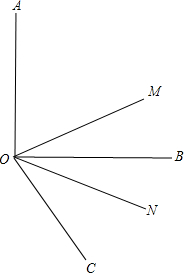 如图,射线OC在∠AOB的外部,∠BOC=a(a为锐角)且OM平分∠AOC,ON平分∠BOC.
如图,射线OC在∠AOB的外部,∠BOC=a(a为锐角)且OM平分∠AOC,ON平分∠BOC.