题目内容
1.若四边形的两条对角线分别平分两组对角,则该四边形一定是( )| A. | 平行四边形 | B. | 菱形 | C. | 矩形 | D. | 正方形 |
分析 由题意得出∠1=∠2=$\frac{1}{2}$∠ABC,∠3=∠4=$\frac{1}{2}$∠ADC,由三角形内角和定理得出∠BAD=∠BCD,同理:∠ABC=∠ADC,证出四边形ABCD是平行四边形,证出∠1=∠3,得出AB=AD,即可得出结论.
解答 解:如图所示:
∵BD平分∠ABC、∠ADC,
∴∠1=∠2=$\frac{1}{2}$∠ABC,∠3=∠4=$\frac{1}{2}$∠ADC,
∵∠BAD+∠1+∠3=180°,∠BCD+∠2+∠4=180°,
∴∠BAD=∠BCD,
同理:∠ABC=∠ADC,
∴四边形ABCD是平行四边形,∠1=∠3,
∴AB=AD,
∴四边形ABCD是菱形.
故选:B.
点评 本题考查了平行四边形的判定、菱形的判定、三角形内角和定理、等腰三角形的判定;熟练掌握菱形的判定,证明四边形是平行四边形是解决问题的关键.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
9.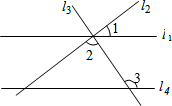 如图,直线l1,l2,l3交于一点,直线l4∥l1,若∠3=124°,∠2=88°,则∠1的度数为( )
如图,直线l1,l2,l3交于一点,直线l4∥l1,若∠3=124°,∠2=88°,则∠1的度数为( )
 如图,直线l1,l2,l3交于一点,直线l4∥l1,若∠3=124°,∠2=88°,则∠1的度数为( )
如图,直线l1,l2,l3交于一点,直线l4∥l1,若∠3=124°,∠2=88°,则∠1的度数为( )| A. | 26° | B. | 36° | C. | 46° | D. | 56° |
6.在?ABCD中,若∠A+∠C=200°,则∠B的大小为( )
| A. | 160° | B. | 100° | C. | 80° | D. | 60° |
10.下列运算正确的是( )
| A. | a0=1 | B. | $\sqrt{9}$=±3 | C. | (ab)2=ab2 | D. | (-a2)3=-a6 |
11. 如图,直线AB∥CD,∠C=115°,∠A=25°,则∠E的度数为( )
如图,直线AB∥CD,∠C=115°,∠A=25°,则∠E的度数为( )
 如图,直线AB∥CD,∠C=115°,∠A=25°,则∠E的度数为( )
如图,直线AB∥CD,∠C=115°,∠A=25°,则∠E的度数为( )| A. | 100° | B. | 90° | C. | 80° | D. | 70° |
 已知:如图,线段a,∠α.
已知:如图,线段a,∠α.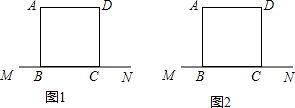 已知正方形ABCD如图所示,M、N在直线BC上,MB=NC,试分别在图1、图2中仅用无刻度的直尺画出一个不同的等腰三角形OMN.
已知正方形ABCD如图所示,M、N在直线BC上,MB=NC,试分别在图1、图2中仅用无刻度的直尺画出一个不同的等腰三角形OMN.