题目内容
9.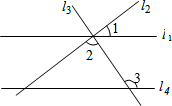 如图,直线l1,l2,l3交于一点,直线l4∥l1,若∠3=124°,∠2=88°,则∠1的度数为( )
如图,直线l1,l2,l3交于一点,直线l4∥l1,若∠3=124°,∠2=88°,则∠1的度数为( )| A. | 26° | B. | 36° | C. | 46° | D. | 56° |
分析 如图,首先运用平行线的性质求出∠4的大小,然后借助平角的定义求出∠1即可解决问题.
解答  解:如图,∵直线l4∥l1,
解:如图,∵直线l4∥l1,
∴∠1+∠AOB=180°,而∠3=124°,
∴∠4=56°,
∴∠1=180°-∠2-∠4
=180°-88°-56°
=36°.
故选B.
点评 主要考查了平行线的性质及其应用问题;应牢固掌握平行线的性质,这是灵活运用、解题的基础和关键.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
19.16的平方根是( )
| A. | 2 | B. | 4 | C. | -2或2 | D. | -4或4 |
20.在平面直角坐标系中,若m为实数,则点(-2,m2+1)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
1.若四边形的两条对角线分别平分两组对角,则该四边形一定是( )
| A. | 平行四边形 | B. | 菱形 | C. | 矩形 | D. | 正方形 |
18.下列计算正确的是( )
| A. | (a-b)2=a2-b2 | B. | 5x2+x3=5x5 | C. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | D. | (a2b)3=a6b3 |
19.已知α、β是方程$\sqrt{2}$x2+$\sqrt{6}$x-1=0的两个实根,则α2+β2=( )
| A. | 3-$\sqrt{2}$ | B. | 3+$\sqrt{2}$ | C. | -3-$\sqrt{2}$ | D. | -3+$\sqrt{2}$ |
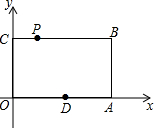 如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(6,0)、(0,4),点P是线段BC上的动点,当△OPA是等腰三角形时,则P点的坐标是(3,4)或(2$\sqrt{5}$,4)或(6-2$\sqrt{5}$,4).
如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(6,0)、(0,4),点P是线段BC上的动点,当△OPA是等腰三角形时,则P点的坐标是(3,4)或(2$\sqrt{5}$,4)或(6-2$\sqrt{5}$,4).