题目内容
等腰梯形的上、下底分别是3cm和5cm,一个角是135°,则等腰梯形的面积为 .
考点:等腰梯形的性质
专题:
分析:作等腰梯形的两条高,然后根据已知条件求出高的长,则可以求出梯形的面积.
解答: 解:如图,∵AD=3cm,BC=5cm,BE=CF=
解:如图,∵AD=3cm,BC=5cm,BE=CF=
(5-3)=1(cm),∠B=∠C=45°,
∴△ABE为等腰直角三角形,
∴BE=AE=1cm,
∴梯形的面积=
(AD+BC)×AE=4(cm2).
故答案为:4cm2.
 解:如图,∵AD=3cm,BC=5cm,BE=CF=
解:如图,∵AD=3cm,BC=5cm,BE=CF=| 1 |
| 2 |
∴△ABE为等腰直角三角形,
∴BE=AE=1cm,
∴梯形的面积=
| 1 |
| 2 |
故答案为:4cm2.
点评:此题主要考查了等腰梯形的性质的理解及运用,得出等腰梯形的高是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
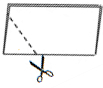 如图,将一张矩形纸片对折两次后剪下一个角,然后打开.如果要剪出一个正方形,那么剪口线与折痕所成的锐角大小是( )
如图,将一张矩形纸片对折两次后剪下一个角,然后打开.如果要剪出一个正方形,那么剪口线与折痕所成的锐角大小是( )| A、22.5° | B、45° |
| C、60° | D、135° |
 在三角形纸片ABC中,∠C=90°,∠A=30°,AC=3,折叠该纸片,使点A与点B重合,折痕与AB、AC分别相交于点D和点E(如图),折痕DE的长为( )
在三角形纸片ABC中,∠C=90°,∠A=30°,AC=3,折叠该纸片,使点A与点B重合,折痕与AB、AC分别相交于点D和点E(如图),折痕DE的长为( )
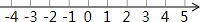 已知在纸面上有一数轴(如图),折叠纸面.例如:若数轴上数2表示的点与数-2表示的点重合,则数轴上数-4表示的点与数4表示的点重合,根据你对例题的理解,解答下列问题:
已知在纸面上有一数轴(如图),折叠纸面.例如:若数轴上数2表示的点与数-2表示的点重合,则数轴上数-4表示的点与数4表示的点重合,根据你对例题的理解,解答下列问题: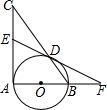 如图,已知Rt△ABC中,∠CAB=90°,以AB为直径的⊙O交斜边BC于点D,E是AC的中点,连接ED并延长交AB的延长线于点F.
如图,已知Rt△ABC中,∠CAB=90°,以AB为直径的⊙O交斜边BC于点D,E是AC的中点,连接ED并延长交AB的延长线于点F.