题目内容
已知
=
=
,求
.
| y+z |
| x |
| z+x |
| y |
| x+y |
| z |
| (y+z)(z+x)(x+y) |
| xyz |
考点:对称式和轮换对称式
专题:计算题
分析:设
=
=
=k,则有y+z=kx①,z+x=ky②,x+y=kz③,
=k3.由①+②+③可求出k=2或-1,就可解决问题.
| y+z |
| x |
| z+x |
| y |
| x+y |
| z |
| (y+z)(z+x)(x+y) |
| xyz |
解答:解:设
=
=
=k,
则有y+z=kx①,z+x=ky②,x+y=kz③,
=k3.
由①+②+③得:2x+2y+2z=kx+ky+kz,
∴2(x+y+z)=k(x+y+z),
∴(k-2)(x+y+z)=0,
∴k=2或x+y+z=0,
∴k=2或k=
=
=-1.
Ⅰ.当k=2时,
=k3=8;
Ⅱ.当k=-1时,
=k3=-1.
综上所述:
的值为8或-1.
| y+z |
| x |
| z+x |
| y |
| x+y |
| z |
则有y+z=kx①,z+x=ky②,x+y=kz③,
| (y+z)(z+x)(x+y) |
| xyz |
由①+②+③得:2x+2y+2z=kx+ky+kz,
∴2(x+y+z)=k(x+y+z),
∴(k-2)(x+y+z)=0,
∴k=2或x+y+z=0,
∴k=2或k=
| y+z |
| x |
| -x |
| x |
Ⅰ.当k=2时,
| (y+z)(z+x)(x+y) |
| xyz |
Ⅱ.当k=-1时,
| (y+z)(z+x)(x+y) |
| xyz |
综上所述:
| (y+z)(z+x)(x+y) |
| xyz |
点评:本题考查的是求轮换对称式的值,运用整体思想是解决本题的关键,需要注意的是:由于x+y+z可能为0,因此在运用等式2(x+y+z)=k(x+y+z)求k的过程中,等式两边不能同时除以x+y+z,只能通过移项并提取公因式来解决问题.

练习册系列答案
相关题目
如图,该图形的相邻两边均互相垂直,则这个图形的周长为( )


| A、37 | B、26 | C、42 | D、21 |
 观察图形(左右分别为平移前后两图形),若图中的点P的坐标为(2.6,2),则它在右图中的对应点P1的坐标为
观察图形(左右分别为平移前后两图形),若图中的点P的坐标为(2.6,2),则它在右图中的对应点P1的坐标为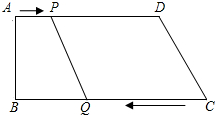 如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AB=8厘米,AD=24厘米,BC=26厘米,动点P从点A开始沿AD边向点D以1厘米/秒的速度运动,动点Q从点C开始沿CB边向点B以3厘米/秒的速度运动,P、Q分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒.问:
如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AB=8厘米,AD=24厘米,BC=26厘米,动点P从点A开始沿AD边向点D以1厘米/秒的速度运动,动点Q从点C开始沿CB边向点B以3厘米/秒的速度运动,P、Q分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒.问: 如图,点P在∠AOB的内部,点M、N分别是点P关于直线OA、OB的对称点,线段MN交OA、OB于点E、F,若△PEF的周长是20cm,
如图,点P在∠AOB的内部,点M、N分别是点P关于直线OA、OB的对称点,线段MN交OA、OB于点E、F,若△PEF的周长是20cm,