题目内容
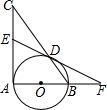 如图,已知Rt△ABC中,∠CAB=90°,以AB为直径的⊙O交斜边BC于点D,E是AC的中点,连接ED并延长交AB的延长线于点F.
如图,已知Rt△ABC中,∠CAB=90°,以AB为直径的⊙O交斜边BC于点D,E是AC的中点,连接ED并延长交AB的延长线于点F.(1)求证:DE为⊙O的切线;
(2)若∠F=30°,AB=4,求DF、EF的长.
考点:切线的判定,勾股定理,相似三角形的判定与性质
专题:
分析:(1)连接BD、DO,只要证明∠ODE=90°,OD是半径,就可得到DE是⊙O的切线.
(2)利用Rt△ODF∽Rt△EAF的性质来求DF、EF的长.
(2)利用Rt△ODF∽Rt△EAF的性质来求DF、EF的长.
解答:(1)证明:连接BD,DO,
∵AB是⊙O的直径,
∴∠ADB=∠CDA=90°
又∵E为AC的中点,
∴CE=EA,
∴∠1=∠4.
∵OD=OA,
∴∠2=∠3.
∴∠1+∠2=∠3+∠4=90°,即∠EDO=90°,
又∵OD是半径,
∴DE是⊙O的切线.
(2)解:由(1)知,∠ODF=90°.
在Rt△ODF中,∠F=30°,OD=
AB=2,
∴OF=4,DF=
=2
.
在Rt△ODF与Rt△EAF中,
∵∠ODF=∠EAF=90°,∠F=∠F,
∴Rt△ODF∽Rt△EAF,
∴
=
,即
=
,
则EF=4
.

∵AB是⊙O的直径,
∴∠ADB=∠CDA=90°
又∵E为AC的中点,
∴CE=EA,
∴∠1=∠4.
∵OD=OA,
∴∠2=∠3.
∴∠1+∠2=∠3+∠4=90°,即∠EDO=90°,
又∵OD是半径,
∴DE是⊙O的切线.
(2)解:由(1)知,∠ODF=90°.
在Rt△ODF中,∠F=30°,OD=
| 1 |
| 2 |
∴OF=4,DF=
| 42-22 |
| 3 |
在Rt△ODF与Rt△EAF中,
∵∠ODF=∠EAF=90°,∠F=∠F,
∴Rt△ODF∽Rt△EAF,
∴
| OF |
| EF |
| DF |
| AF |
| 4 |
| EF |
2
| ||
| 6 |
则EF=4
| 3 |
点评:本题利用了切线的判定和性质,相似三角形的判定和性质.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目

 观察图形(左右分别为平移前后两图形),若图中的点P的坐标为(2.6,2),则它在右图中的对应点P1的坐标为
观察图形(左右分别为平移前后两图形),若图中的点P的坐标为(2.6,2),则它在右图中的对应点P1的坐标为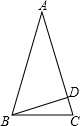 如图,等腰△ABC中,AB=AC,BD是腰AC上的高线,∠DBC=15°,若BD=5,则AC等于
如图,等腰△ABC中,AB=AC,BD是腰AC上的高线,∠DBC=15°,若BD=5,则AC等于