题目内容
 在三角形纸片ABC中,∠C=90°,∠A=30°,AC=3,折叠该纸片,使点A与点B重合,折痕与AB、AC分别相交于点D和点E(如图),折痕DE的长为( )
在三角形纸片ABC中,∠C=90°,∠A=30°,AC=3,折叠该纸片,使点A与点B重合,折痕与AB、AC分别相交于点D和点E(如图),折痕DE的长为( )| A、1 | ||
| B、2 | ||
| C、3 | ||
D、
|
考点:翻折变换(折叠问题)
专题:
分析:由折叠可得△ADE≌△BDE≌△BCE,易得AD的值,进而根据30°的三角函数值可得DE的值.
解答:解:∵∠C=90°,∠A=30°,AC=3,
∴AB=AC÷cosA=2
,
∴AD=BD=
,
由折叠可得∠ADE=90°,
∴DE=AD×tan30°=1.
故选:A.
∴AB=AC÷cosA=2
| 3 |
∴AD=BD=
| 3 |
由折叠可得∠ADE=90°,
∴DE=AD×tan30°=1.
故选:A.
点评:此题考查折叠问题,判断出所求线段所在的三角形的形状及相关线段长是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
函数y=
的自变量取值范围为( )
| ||
| 2 |
| A、x≤1 | B、x≤-1 |
| C、x>1 | D、x≥-1 |
如果两个角的两边互相平行,那么这两个角( )
| A、相等 | B、互余 |
| C、相等或互补 | D、互补 |
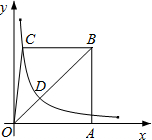 如图,梯形ABCO的底边AO在x轴上,BC∥AO,AB⊥AO,反比例函数y=
如图,梯形ABCO的底边AO在x轴上,BC∥AO,AB⊥AO,反比例函数y=
 如图,点P在∠AOB的内部,点M、N分别是点P关于直线OA、OB的对称点,线段MN交OA、OB于点E、F,若△PEF的周长是20cm,
如图,点P在∠AOB的内部,点M、N分别是点P关于直线OA、OB的对称点,线段MN交OA、OB于点E、F,若△PEF的周长是20cm,