题目内容
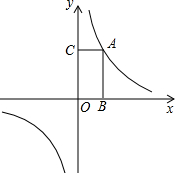 如图,函数y=
如图,函数y=| k |
| x |
(1)求该函数的解析式;
(2)过点A分别向x轴和y轴作垂线,垂足为B和C,求四边形ABOC的面积;
(3)求证:过此函数图象上任意一点分别向x轴和y轴作垂线,这两条垂线与两坐标轴所围成矩形的面积为定值.
考点:待定系数法求反比例函数解析式,反比例函数系数k的几何意义
专题:
分析:(1)将点A的坐标代入反比例函数解析式,即可求出k值;
(2)由于点A是反比例函数上一点,矩形ABOC的面积S=|k|.
(3)设图象上任一点的坐标(x,y),根据矩形的面积公式,可得出结论.
(2)由于点A是反比例函数上一点,矩形ABOC的面积S=|k|.
(3)设图象上任一点的坐标(x,y),根据矩形的面积公式,可得出结论.
解答:解:(1)∵函数y=
的图象过点A(1,2),
∴将点A的坐标代入反比例函数解析式,
得2=
,解得:k=2,
∴反比例函数的解析式为y=
;
(2)∵点A是反比例函数上一点,
∴矩形ABOC的面积S=AC•AB=|xy|=|k|=2.
(3)设图象上任一点的坐标(x,y),
∴过这点分别向x轴和y轴作垂线,矩形面积为|xy|=|k|=2,
∴矩形的面积为定值.
| k |
| x |
∴将点A的坐标代入反比例函数解析式,
得2=
| k |
| 1 |
∴反比例函数的解析式为y=
| 2 |
| x |
(2)∵点A是反比例函数上一点,
∴矩形ABOC的面积S=AC•AB=|xy|=|k|=2.
(3)设图象上任一点的坐标(x,y),
∴过这点分别向x轴和y轴作垂线,矩形面积为|xy|=|k|=2,
∴矩形的面积为定值.
点评:本题主要考查了待定系数法求反比例函数解析式和反比例函数y=
中k的几何意义,注意掌握过双曲线上任意一点引x轴、y轴垂线,所得矩形面积为|k|,是经常考查的一个知识点.
| k |
| x |

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
不等式组2≤3x-7<9的所有整数解为( )
| A、3,4 | B、4,5 |
| C、3,4,5 | D、3,4,5,6 |
 如图,在矩形ABCD中,AD=9cm,AB=3cm,将其折叠,使点D和点B重合,则重叠部分(△BEF)的面积为
如图,在矩形ABCD中,AD=9cm,AB=3cm,将其折叠,使点D和点B重合,则重叠部分(△BEF)的面积为 如图,在?ABCD中,E是BC的延长线上一点,AE与CD交于点F,BC=2CE.若AB=6,则DF的长为( )
如图,在?ABCD中,E是BC的延长线上一点,AE与CD交于点F,BC=2CE.若AB=6,则DF的长为( )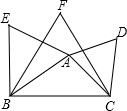 如图,根据图形解答下列问题
如图,根据图形解答下列问题 如图,已知△ABC中,AB=AC,E,D,F分别是边AB,BC,AC的中点.
如图,已知△ABC中,AB=AC,E,D,F分别是边AB,BC,AC的中点.