题目内容
 如图,已知△ABC中,AB=AC,E,D,F分别是边AB,BC,AC的中点.
如图,已知△ABC中,AB=AC,E,D,F分别是边AB,BC,AC的中点.(1)求证:四边形AEDF是菱形;
(2)若∠B=30°,BC=6,求四边形AEDF的周长.
考点:菱形的判定与性质,三角形中位线定理
专题:
分析:(1)首先根据三角形中位线定理可得DE∥AC,DF∥AB,ED=
AC,DF=
AB,进而可判定四边形AEDF是平行四边形,然后证明ED=DF即可;
(2)过E作EM⊥BD,根据题意可得BD长,然后再根据等腰三角形的性质可得BM=
BD=1.5,然后再利用勾股定理可得ED长,进而可得菱形周长.
| 1 |
| 2 |
| 1 |
| 2 |
(2)过E作EM⊥BD,根据题意可得BD长,然后再根据等腰三角形的性质可得BM=
| 1 |
| 2 |
解答:(1)证明:∵E,D,F分别是边AB,BC,AC的中点,
∴DE∥AC,DF∥AB,ED=
AC,DF=
AB,
∴四边形AEDF是平行四边形,
∵AB=AC,
∴ED=DF,
∴四边形AEDF是菱形;
(2)解:过E作EM⊥BD,
∵E为AB中点,
∴AE=EB,
∵四边形AEDF是菱形,
∴AE=ED=EB,
∵BC=6,D是BC中点,
∴DB=3,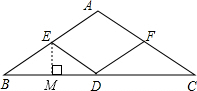
∵EM⊥BD,
∴BM=
BD=1.5,
∵∠B=30°,
∴EM=
BE,
∵EM2+MB2=EB2,
∴(
EB)2+MB2=EB2,
∴BE=
,
∴ED=
,
∴四边形AEDF的周长为4
.
∴DE∥AC,DF∥AB,ED=
| 1 |
| 2 |
| 1 |
| 2 |
∴四边形AEDF是平行四边形,
∵AB=AC,
∴ED=DF,
∴四边形AEDF是菱形;
(2)解:过E作EM⊥BD,
∵E为AB中点,
∴AE=EB,
∵四边形AEDF是菱形,
∴AE=ED=EB,
∵BC=6,D是BC中点,
∴DB=3,

∵EM⊥BD,
∴BM=
| 1 |
| 2 |
∵∠B=30°,
∴EM=
| 1 |
| 2 |
∵EM2+MB2=EB2,
∴(
| 1 |
| 2 |
∴BE=
| 3 |
∴ED=
| 3 |
∴四边形AEDF的周长为4
| 3 |
点评:此题主要考查了菱形的判定和性质,关键是掌握邻边相等的平行四边形是菱形,菱形四边相等.

练习册系列答案
相关题目
在
、
、
、
、中,与
是同类二次根式的有( )
| 8 |
| 12 |
| 27 |
| 32 |
| 3 |
| A、1个 | B、2个 | C、3个 | D、4个 |
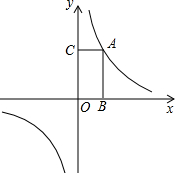 如图,函数y=
如图,函数y=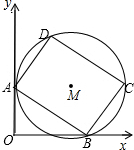 如图,圆M为矩形ABCD的外接圆,AD=6,AB=8,矩形ABCD的两个顶点A,B,分别在y轴,x轴的正半轴上滑动,保持AB的长度不变.
如图,圆M为矩形ABCD的外接圆,AD=6,AB=8,矩形ABCD的两个顶点A,B,分别在y轴,x轴的正半轴上滑动,保持AB的长度不变. 如图,在△ABC中,BD⊥AC,AB=6,AC=5
如图,在△ABC中,BD⊥AC,AB=6,AC=5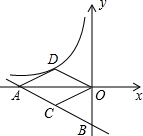 如图,一次函数y=-
如图,一次函数y=-