题目内容
 如图,在?ABCD中,E是BC的延长线上一点,AE与CD交于点F,BC=2CE.若AB=6,则DF的长为( )
如图,在?ABCD中,E是BC的延长线上一点,AE与CD交于点F,BC=2CE.若AB=6,则DF的长为( )| A、2 | B、3 | C、4 | D、5 |
考点:平行四边形的性质,相似三角形的判定与性质
专题:
分析:由在?ABCD中,BC=2CE.AB=6,根据平行四边形的性质,可得AD∥BC,CD=AB=6,AD=BC,继而可证得△ADF∽△ECF,然后由相似三角形的对应边成比例,求得答案.
解答:解:∵四边形ABCD是平行四边形,
∴AD∥BC,CD=AB=6,AD=BC,
∴△ADF∽△ECF,
∴DF:CF=AD:CE,
∵BC=2CE,
∴DF:CF=AD:CE=2,
∴DF=
CD=
×6=4.
故选C.
∴AD∥BC,CD=AB=6,AD=BC,
∴△ADF∽△ECF,
∴DF:CF=AD:CE,
∵BC=2CE,
∴DF:CF=AD:CE=2,
∴DF=
| 2 |
| 3 |
| 2 |
| 3 |
故选C.
点评:此题考查了相似三角形的判定与性质以及平行四边形的性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
 如图是由5个大小相同的小正方体摆成的立体图形,它的俯视图是( )
如图是由5个大小相同的小正方体摆成的立体图形,它的俯视图是( )A、 |
B、 |
C、 |
D、 |
2014年1月30日晚,全国约有7.04亿人观看中央电视台播出的马年春节联欢晚会,7.04亿用科学记数法可表示为( )
| A、7.04×107 |
| B、7.04×108 |
| C、7.04×109 |
| D、7.04×1010 |
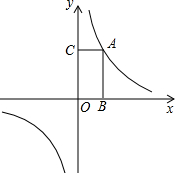 如图,函数y=
如图,函数y=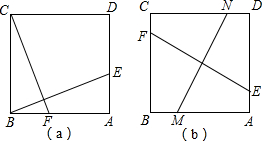 已知正方形ABCD,点E、F分别是AD、AB边上的点,且BE⊥CF;
已知正方形ABCD,点E、F分别是AD、AB边上的点,且BE⊥CF;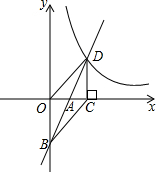 如图,在平面直角坐标系中,一次函数y=2x+b(b<0)的图象与坐标轴交于A、B两点,与函数y=
如图,在平面直角坐标系中,一次函数y=2x+b(b<0)的图象与坐标轴交于A、B两点,与函数y=