题目内容
7.己知$\frac{y}{x}-\frac{x}{y}$=-5,求分式$\frac{{3x}^{2}+xy-{3y}^{2}}{{2x}^{2}-xy-{2y}^{2}}$的值.分析 将已知变形进而得出x2-y2=5xy,再整体代入原式求出答案.
解答 解:∵$\frac{y}{x}-\frac{x}{y}$=-5,
∴$\frac{{y}^{2}-{x}^{2}}{xy}$=-5,
∴y2-x2=-5xy,
则x2-y2=5xy
∴$\frac{{3x}^{2}+xy-{3y}^{2}}{{2x}^{2}-xy-{2y}^{2}}$=$\frac{3({x}^{2}-{y}^{2})+xy}{2({x}^{2}-{y}^{2})-xy}$=$\frac{3×5xy+xy}{2×5xy-xy}$=$\frac{16}{9}$.
点评 此题主要考查了分式的化简求值,正确将已知变形是解题关键.

练习册系列答案
相关题目
16.某商场为提高彩电销售人员的积极性,制定了新的工资分配方案.方案规定:每位销售人员的工资总额=基本工资+奖励工资.每位销售人员的月销售定额为10000元,在销售定额内,得基本工资200元;超过销售定额,超过部分的销售额按相应比例作为奖励工资.
(1)已知销售员甲本月分领到的工资总额为800元,请问甲本月的销售额为多少元?
(2)若销售员乙本月得到工资1300元,问乙本月的销售额为多少元?
(3)在(2)的条件下,已知乙本月销售A、B两种型号的彩电21台,且A型彩电的销售价为每台1000元,B型彩电的销售价为每台1500元,问乙本月销售A型彩电多少台?
(1)已知销售员甲本月分领到的工资总额为800元,请问甲本月的销售额为多少元?
(2)若销售员乙本月得到工资1300元,问乙本月的销售额为多少元?
(3)在(2)的条件下,已知乙本月销售A、B两种型号的彩电21台,且A型彩电的销售价为每台1000元,B型彩电的销售价为每台1500元,问乙本月销售A型彩电多少台?
| 销售额 | 奖励工资比例 |
| 超过0元但不超过5千元部分 | 5% |
| 超过0.5万元但不超过1万元部分 | 8% |
| 1万元以上的部分 | 10% |
7.若二次根式$\sqrt{\frac{1}{3-2a}}$有意义,则字母a应满足的条件是( )
| A. | $a<\frac{3}{2}$ | B. | $a≤\frac{3}{2}$ | C. | $a>\frac{3}{2}$ | D. | $a≥\frac{3}{2}$ |
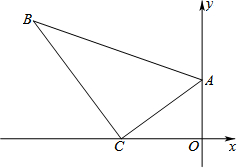 如图,一块直角三角板ABC放置在平面直角坐标系中,∠B=30°,顶点A的坐标为(0,6),直角顶点C的坐标为(-8,0).
如图,一块直角三角板ABC放置在平面直角坐标系中,∠B=30°,顶点A的坐标为(0,6),直角顶点C的坐标为(-8,0).