题目内容
18.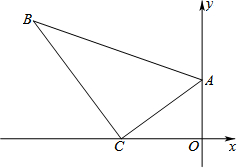 如图,一块直角三角板ABC放置在平面直角坐标系中,∠B=30°,顶点A的坐标为(0,6),直角顶点C的坐标为(-8,0).
如图,一块直角三角板ABC放置在平面直角坐标系中,∠B=30°,顶点A的坐标为(0,6),直角顶点C的坐标为(-8,0).(1)求点A、C所在直线的解析式;
(2)求点B的坐标;
(3)在直线AC上是否存在点D,使以A、B、D为顶点的三角形为等腰三角形?若存在,请直接写出点D的坐标;若不存在,不必说明理由.
分析 (1)设出直线AC的解析式为y=kx+b,由A、C点的坐标,利用待定系数法即可得出结论;
(2)过点B作BD⊥x轴于点D,由∠BCD与∠ACO互余以及∠ACO与∠OAC互余可知∠BCD=∠OAC;在Rt△AOC中由已知的边长可以求出AC的长度即∠OAC的正弦和余弦值;在Rt△BCA中由∠ABC=30°和AC的长度可得出BC以及AB的长度;在Rt△BDC中,由BC的长度以及∠BCD的正弦余弦值可得出CD、BD的长度,从而能得出点B的坐标;
(3)假设存在,由点D在直线AC上可设出点D的坐标为(m,$\frac{3}{4}$m+6),由两点间的距离公式结合等腰三角形的性质列出关于m的一元二次方程,解方程可以得出结论.
解答 解:(1)设点A、C所在直线的解析式为y=kx+b,
∵A点坐标为(0,6),C点坐标为(-8,0),
∴有$\left\{\begin{array}{l}{6=b}\\{0=-8k+b}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=\frac{3}{4}}\\{b=6}\end{array}\right.$.
故点A、C所在直线的解析式为y=$\frac{3}{4}$x+6.
(2)过点B作BD⊥x轴于点D,如图所示.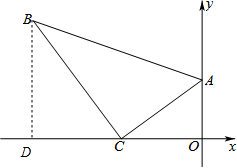
∵A点坐标为(0,6),C点坐标为(-8,0),
∴OA=6,OC=8,AC=$\sqrt{O{A}^{2}+O{C}^{2}}$=10.
又∵∠ABC=30°,∠ACB=90°,
∴AB=$\frac{AC}{sin∠ABC}$=20,BC=$\frac{AC}{tan∠ABC}$=10$\sqrt{3}$.
∵∠BCD+∠BCA+∠ACO=180°,∠ACO+∠OAC=90°,
∴∠BCD=∠OAC.
在Rt△AOC中,OA=6,OC=8,AC=10,∠AOC=90°,
∴sin∠OAC=$\frac{OC}{AC}$=$\frac{4}{5}$,cos∠OAC=$\frac{OA}{AC}$=$\frac{3}{5}$.
在Rt△BDC中,BC=10$\sqrt{3}$,
∴BD=BC•sin∠BCD=8$\sqrt{3}$,CD=BC•cos∠BCD=6$\sqrt{3}$,
OD=OC+CD=8+6$\sqrt{3}$.
故点B的坐标为(-8-6$\sqrt{3}$,8$\sqrt{3}$).
(3)假设存在,
∵点D在直线AC上,
∴设点D的坐标为(m,$\frac{3}{4}$m+6).
∵点A(0,6),点B(-8-6$\sqrt{3}$,8$\sqrt{3}$),
∴由两点间的距离公式可知:AB=20,AD=$\sqrt{{m}^{2}+(\frac{3}{4}m)^{2}}$,BD=$\sqrt{(m+8+6\sqrt{3})^{2}+(\frac{3}{4}m+6-8\sqrt{3})^{2}}$.
以A、B、D为顶点的三角形为等腰三角形有三种情况:
①AB=AD,即20=$\sqrt{{m}^{2}+(\frac{3}{4}m)^{2}}$,
解得:m=±16,
此时点D的坐标为(16,18)或(-16,-6);
②AB=BD,即20=$\sqrt{(m+8+6\sqrt{3})^{2}+(\frac{3}{4}m+6-8\sqrt{3})^{2}}$,
解得:m=-16,或m=0(舍去),
此时点D的坐标为(-16,-6);
③AD=BD,即$\sqrt{{m}^{2}+(\frac{3}{4}m)^{2}}$=$\sqrt{(m+8+6\sqrt{3})^{2}+(\frac{3}{4}m+6-8\sqrt{3})^{2}}$,
解得:m=-16,
此时点D的坐标为(-16,-6).
综上所述:在直线AC上存在点D,使以A、B、D为顶点的三角形为等腰三角形,点D的坐标为(16,18)或(-16,-6).
点评 本题考查了待定系数法求函数解析式、两点间的距离公式、等腰三角形的性质以及解直角三角形,解题的关键是:(1)利用待定系数法求解析式;(2)通过解直角三角形得出结论;(3)由两点间的距离公式结合等腰三角形的性质得出关于m的一元二次方程.本题属于中档题,难度不大,(1)没有难度;(2)需要借助三角函数值解直角三角形,也可以找相似三角形,根据相似三角形的性质找出比例关系;(3)设出点D坐标根据两点间的距离公式去列方程,其实在解决(3)时由∠BAC=60°可知等腰三角形其实为等边三角形.

 优生乐园系列答案
优生乐园系列答案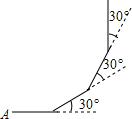 如图:小明从点A出发,沿直线前进5m后向左转30°,再沿直线前进5m后,又向左转30°,照这样方式走下去,他第一次回到出发点A时,一共走了( )
如图:小明从点A出发,沿直线前进5m后向左转30°,再沿直线前进5m后,又向左转30°,照这样方式走下去,他第一次回到出发点A时,一共走了( )| A. | 50m | B. | 60m | C. | 70m | D. | 80m |
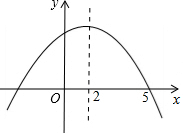 如图,对于二次函数y=ax2+bx+c(a≠0)在x轴上方的图象,当y随x增大而增大时,x的取值范围是( )
如图,对于二次函数y=ax2+bx+c(a≠0)在x轴上方的图象,当y随x增大而增大时,x的取值范围是( )| A. | x<-1 | B. | -1<x<2 | C. | 2<x<5 | D. | x>5 |
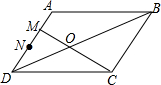 在?ABCD中,M,N是AD边上的三等分点,连接BD,MC相交于O点,则$\frac{{S}_{△MOD}}{{S}_{△COB}}$=( )
在?ABCD中,M,N是AD边上的三等分点,连接BD,MC相交于O点,则$\frac{{S}_{△MOD}}{{S}_{△COB}}$=( )| A. | $\frac{1}{9}$或$\frac{4}{9}$ | B. | $\frac{1}{9}$ | C. | $\frac{4}{9}$ | D. | $\frac{1}{3}$或$\frac{2}{3}$ |
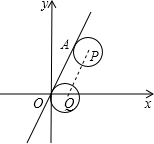 如图,在平面直角坐标系中,直线l经过原点以及点A(1,$\sqrt{3}$),圆P与直线l相切于点A,若圆P沿直线l滚动一周,点A恰好与原点重合,此时圆心位于点Q,则点Q的坐标为( )
如图,在平面直角坐标系中,直线l经过原点以及点A(1,$\sqrt{3}$),圆P与直线l相切于点A,若圆P沿直线l滚动一周,点A恰好与原点重合,此时圆心位于点Q,则点Q的坐标为( )| A. | ($\frac{1}{2π},-\frac{\sqrt{3}}{π}$) | B. | ($\frac{1}{π},-\frac{\sqrt{3}}{π}$) | C. | ($\frac{\sqrt{3}}{2},-\frac{1}{2}$) | D. | ($\frac{\sqrt{3}}{2π},-\frac{1}{2π}$) |
 如图,已知△ABC的三个顶点均在正方形网格的格点上,则cosA的值为$\frac{2\sqrt{5}}{5}$.
如图,已知△ABC的三个顶点均在正方形网格的格点上,则cosA的值为$\frac{2\sqrt{5}}{5}$.