题目内容
16.某商场为提高彩电销售人员的积极性,制定了新的工资分配方案.方案规定:每位销售人员的工资总额=基本工资+奖励工资.每位销售人员的月销售定额为10000元,在销售定额内,得基本工资200元;超过销售定额,超过部分的销售额按相应比例作为奖励工资.(1)已知销售员甲本月分领到的工资总额为800元,请问甲本月的销售额为多少元?
(2)若销售员乙本月得到工资1300元,问乙本月的销售额为多少元?
(3)在(2)的条件下,已知乙本月销售A、B两种型号的彩电21台,且A型彩电的销售价为每台1000元,B型彩电的销售价为每台1500元,问乙本月销售A型彩电多少台?
| 销售额 | 奖励工资比例 |
| 超过0元但不超过5千元部分 | 5% |
| 超过0.5万元但不超过1万元部分 | 8% |
| 1万元以上的部分 | 10% |
分析 (1)首先计算出当销售额为15000元时,工资总额;当销售额为20000元时,工资总额,从而确定甲本月的销售额的范围,再设销售员甲该月的销售额为x元,利用基本工资+5000元的5%的奖励+超过15000的部分的奖励=800,再解方程可得答案;
(2)首先根据题意讨论乙该月的销售额的范围超过20000元,再根据题意可得等量关系:基本工资+5000元的5%的奖励+5000的8%部分的奖励+超过20000元的10%的奖励=1300元;
(3)根据等量关系列出方程组,再根据销售额计算销售A种型号的彩电数量.
解答 解:(1)当销售额为15000元时,工资总额=200+5000×5%=450(元);
当销售额为20000元时,工资总额=200+5000×5%+5000×8%=850(元);
450<800<850,
设销售员甲该月的销售额为x元,则200+5000×5%+(x-15000)×8%=800,
解得:x=19375;
故销售员甲该月的销售额为19375元;
(2)因为工资总额超过850元,所以销售额在10000元以上,
设销售员乙该月的销售额为y元,由题意得:
200+5000×5%+5000×8%+(y-20000)×10%=1300,
解得:y=24500,
故销售员乙该月的销售额为24500元;
(3)设乙销售员本月销售A型彩电a台,销售B型彩电b台,由题意得:
$\left\{\begin{array}{l}{a+b=21}\\{1000a+1500b=24500}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=14}\\{b=7}\end{array}\right.$,
答:乙销售员本月销售A型彩电14台.
点评 此题主要考查了一元一次方程的应用以及二元一次方程组的应用,关键是正确理解题意,找出题目中的等量关系,列出方程.

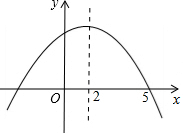 如图,对于二次函数y=ax2+bx+c(a≠0)在x轴上方的图象,当y随x增大而增大时,x的取值范围是( )
如图,对于二次函数y=ax2+bx+c(a≠0)在x轴上方的图象,当y随x增大而增大时,x的取值范围是( )| A. | x<-1 | B. | -1<x<2 | C. | 2<x<5 | D. | x>5 |
①不相交的直线叫做平行线;②两直线平行,同旁内角相等;③相等的角是对顶角;④过一点有且只有一条直线与已知直线垂直;⑤垂线段最短;⑥平方根等于本身的数是0和1;⑦邻补角是互补的角,这句话是一个假命题.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | $\left\{{\begin{array}{l}{2x-2y=18}\\{5x+4y=18}\end{array}}\right.$ | B. | $\left\{{\begin{array}{l}{2x+2y=18}\\{5x-4y=18}\end{array}}\right.$ | ||
| C. | $\left\{{\begin{array}{l}{2x+2y=18}\\{5x=4y-18}\end{array}}\right.$ | D. | $\left\{{\begin{array}{l}{2x+2y=18}\\{5x+4y=18}\end{array}}\right.$ |
 如图,AB∥CD,∠A=50°,∠1-∠2=30°,求∠1的度数.
如图,AB∥CD,∠A=50°,∠1-∠2=30°,求∠1的度数.