题目内容
19.用适当方法解下列方程组:(1)$\left\{\begin{array}{l}{2x+y=4}\\{x+2y=5}\end{array}\right.$,
(2)$\left\{\begin{array}{l}{x+3y=4}\\{\frac{1}{4}x+\frac{1}{2}y=0}\end{array}\right.$.
分析 (1)利用代入消元法将二元一次方程组转化为一元一次方程,进而解方程组求出答案;
(2)利用代入消元法将二元一次方程组转化为一元一次方程,进而解方程组求出答案.
解答 解:(1)$\left\{\begin{array}{l}{2x+y=4①}\\{x+2y=5②}\end{array}\right.$,
由①得:y=4-2x③,
把③代入②得:x+2(4-2x)=5,
解得:x=1,
则y=2,
故二元一次方程组的解为:$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{x+3y=4①}\\{\frac{1}{4}x+\frac{1}{2}y=0②}\end{array}\right.$,
由①得:x=4-3y③,
把③代入②得:$\frac{1}{4}$(4-3y)+$\frac{1}{2}$y=0,
解得:y=4,
则x=4-3×4=-8,
故二元一次方程组的解为:$\left\{\begin{array}{l}{x=-8}\\{y=4}\end{array}\right.$.
点评 此题主要考查了二元一次方程组的解法,正确利用代入消元法解方程组是解题关键.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
9.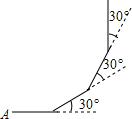 如图:小明从点A出发,沿直线前进5m后向左转30°,再沿直线前进5m后,又向左转30°,照这样方式走下去,他第一次回到出发点A时,一共走了( )
如图:小明从点A出发,沿直线前进5m后向左转30°,再沿直线前进5m后,又向左转30°,照这样方式走下去,他第一次回到出发点A时,一共走了( )
 如图:小明从点A出发,沿直线前进5m后向左转30°,再沿直线前进5m后,又向左转30°,照这样方式走下去,他第一次回到出发点A时,一共走了( )
如图:小明从点A出发,沿直线前进5m后向左转30°,再沿直线前进5m后,又向左转30°,照这样方式走下去,他第一次回到出发点A时,一共走了( )| A. | 50m | B. | 60m | C. | 70m | D. | 80m |
10.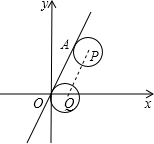 如图,在平面直角坐标系中,直线l经过原点以及点A(1,$\sqrt{3}$),圆P与直线l相切于点A,若圆P沿直线l滚动一周,点A恰好与原点重合,此时圆心位于点Q,则点Q的坐标为( )
如图,在平面直角坐标系中,直线l经过原点以及点A(1,$\sqrt{3}$),圆P与直线l相切于点A,若圆P沿直线l滚动一周,点A恰好与原点重合,此时圆心位于点Q,则点Q的坐标为( )
 如图,在平面直角坐标系中,直线l经过原点以及点A(1,$\sqrt{3}$),圆P与直线l相切于点A,若圆P沿直线l滚动一周,点A恰好与原点重合,此时圆心位于点Q,则点Q的坐标为( )
如图,在平面直角坐标系中,直线l经过原点以及点A(1,$\sqrt{3}$),圆P与直线l相切于点A,若圆P沿直线l滚动一周,点A恰好与原点重合,此时圆心位于点Q,则点Q的坐标为( )| A. | ($\frac{1}{2π},-\frac{\sqrt{3}}{π}$) | B. | ($\frac{1}{π},-\frac{\sqrt{3}}{π}$) | C. | ($\frac{\sqrt{3}}{2},-\frac{1}{2}$) | D. | ($\frac{\sqrt{3}}{2π},-\frac{1}{2π}$) |
19.下列计算正确的是( )
| A. | $\sqrt{36}=±6$ | B. | $4\sqrt{2}÷2\sqrt{2}$=$2\sqrt{2}$ | C. | $8\sqrt{3}-2\sqrt{6}$=6 | D. | $\sqrt{a}•\sqrt{b}=\sqrt{ab}$(a≥0,b≥0) |