题目内容
12.先因式分解,然后计算求值:(1)2x2+2x+$\frac{1}{2}$,其中x=$\frac{11}{4}$;
(2)(x+1)(x+2)+$\frac{1}{4}$,其中x=-$\frac{5}{2}$.
分析 (1)首先提取公因式2,进而利用完全平方公式分解因式求出答案;
(2)首先去括号,进而利用完全平方公式分解因式,进而求出答案.
解答 解:(1)2x2+2x+$\frac{1}{2}$,
=2(x2+x+$\frac{1}{4}$)
=2(x+$\frac{1}{2}$)2
把x=$\frac{11}{4}$代入得:
原式=2×($\frac{11}{4}$+$\frac{1}{2}$)2=2×$\frac{169}{16}$=$\frac{169}{8}$;
(2)(x+1)(x+2)+$\frac{1}{4}$,
=x2+3x+2+$\frac{1}{4}$
=(x+$\frac{3}{2}$)2,
把x=-$\frac{5}{2}$代入得:
原式=(-$\frac{5}{2}$+$\frac{3}{2}$)2=1.
点评 本题考查了因式分解的应用,正确应用因式分解法将原式变形是解题关键.

练习册系列答案
相关题目
3.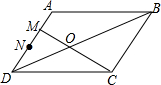 在?ABCD中,M,N是AD边上的三等分点,连接BD,MC相交于O点,则$\frac{{S}_{△MOD}}{{S}_{△COB}}$=( )
在?ABCD中,M,N是AD边上的三等分点,连接BD,MC相交于O点,则$\frac{{S}_{△MOD}}{{S}_{△COB}}$=( )
 在?ABCD中,M,N是AD边上的三等分点,连接BD,MC相交于O点,则$\frac{{S}_{△MOD}}{{S}_{△COB}}$=( )
在?ABCD中,M,N是AD边上的三等分点,连接BD,MC相交于O点,则$\frac{{S}_{△MOD}}{{S}_{△COB}}$=( )| A. | $\frac{1}{9}$或$\frac{4}{9}$ | B. | $\frac{1}{9}$ | C. | $\frac{4}{9}$ | D. | $\frac{1}{3}$或$\frac{2}{3}$ |
17.如果x2+(a+b)•x+5b=x2-x-30,则b为( )
| A. | 5 | B. | -6 | C. | -5 | D. | 6 |
1.下列说法正确的个数有( )
①不相交的直线叫做平行线;②两直线平行,同旁内角相等;③相等的角是对顶角;④过一点有且只有一条直线与已知直线垂直;⑤垂线段最短;⑥平方根等于本身的数是0和1;⑦邻补角是互补的角,这句话是一个假命题.
①不相交的直线叫做平行线;②两直线平行,同旁内角相等;③相等的角是对顶角;④过一点有且只有一条直线与已知直线垂直;⑤垂线段最短;⑥平方根等于本身的数是0和1;⑦邻补角是互补的角,这句话是一个假命题.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
12.一个三角形的三边之比为5:12:13,它的周长为60,则它的面积是( )
| A. | 120 | B. | 144 | C. | 196 | D. | 60 |