题目内容
2.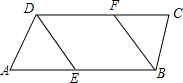 如图,已知∠ABC=∠ADC,BF、DE分别平分∠ABC,∠ADC,且∠AED=∠ABF,求证:∠A=∠C.
如图,已知∠ABC=∠ADC,BF、DE分别平分∠ABC,∠ADC,且∠AED=∠ABF,求证:∠A=∠C.证明:∵BF,DE分别平分∠ABC,∠ADC(已知)
∴∠ABF=$\frac{1}{2}$∠ABC,∠CDE=$\frac{1}{2}$∠ADC(角平分线的定义)
∵∠ABC=∠ADC=(已知)
∴∠ABF=∠CDE(等式的性质)
∵∠AED=∠ABF(已知)
∴∠AED=∠CDE(等量代换)
∴AB∥CD(内错角相等,两直线平行)
∴∠A+∠ADC=180°,∠C+∠ABC=180°(两直线平行,同旁内角互补)
∵∠ABC=∠ADC(已知)
∴∠A=∠C(等式的性质)
分析 由角平分线的性质与∠ABC=∠ADC,∠AED=∠ABF,易证得∠AED=∠CDE,即可证得AB∥CD,继而证得结论.
解答 证明:∵BF,DE分别平分∠ABC,∠ADC(已知)
∴∠ABF=$\frac{1}{2}$∠ABC,∠CDE=$\frac{1}{2}$∠ADC(角平分线的定义)
∵∠ABC=∠ADC=(已知)
∴∠ABF=∠CDE(等式的性质)
∵∠AED=∠ABF(已知)
∴∠AED=∠CDE(等量代换)
∴AB∥CD(内错角相等,两直线平行)
∴∠A+∠ADC=180°,∠C+∠ABC=180°(两直线平行,同旁内角互补)
∵∠ABC=∠ADC(已知)
∴∠A=∠C(等式的性质).
故答案为:已知;角平分线的定义;已知;等式的性质;已知;等量代换;内错角相等,两直线平行;两直线平行,同旁内角互补;等式的性质.
点评 此题考查了平行线的性质与判定.注意掌握内错角相等,两直线平行与两直线平行,同旁内角互补的应用是解此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
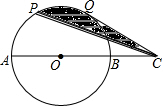 如图,P,Q是半圆O的三等分点,C是直径AB延长线上的一点,若AB=6cm,求阴影部分的面积.
如图,P,Q是半圆O的三等分点,C是直径AB延长线上的一点,若AB=6cm,求阴影部分的面积. 如图,已知直线l1,l2,l3被直线l所截,∠1=72°,∠2=108°,∠3=72°,试说明l1∥l2∥l3.
如图,已知直线l1,l2,l3被直线l所截,∠1=72°,∠2=108°,∠3=72°,试说明l1∥l2∥l3.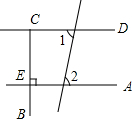 如图,根据图形填空,其中横线上填上结论,括号中填推理理由.
如图,根据图形填空,其中横线上填上结论,括号中填推理理由. 如图,为了估算河的宽度,我们可以在河对岸选定一个目标点A,再在河岸的这一边选取点B和点C,使AB⊥BC,然后再选取点E,使EC⊥BC,用视线确定BC和AE的交点D,此时如果测得BD=160m,DC=80m,EC=50m,求A、B间的大致距离.
如图,为了估算河的宽度,我们可以在河对岸选定一个目标点A,再在河岸的这一边选取点B和点C,使AB⊥BC,然后再选取点E,使EC⊥BC,用视线确定BC和AE的交点D,此时如果测得BD=160m,DC=80m,EC=50m,求A、B间的大致距离.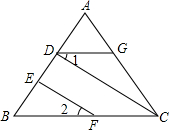 如图,CD⊥AB,EF⊥AB,∠1=∠2,DG与BC平行吗?为什么?
如图,CD⊥AB,EF⊥AB,∠1=∠2,DG与BC平行吗?为什么?