题目内容
13.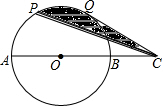 如图,P,Q是半圆O的三等分点,C是直径AB延长线上的一点,若AB=6cm,求阴影部分的面积.
如图,P,Q是半圆O的三等分点,C是直径AB延长线上的一点,若AB=6cm,求阴影部分的面积.
分析 首先连接PO、QO,易得△POQ是等边三角形,又由PQ∥AB,可得S△CPQ=S△POQ,即可得S阴影=S扇形POQ.
解答 解:连接OP、OQ、PQ,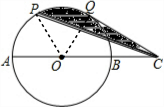
∵P、Q是半圆AB的两个三等分点,
∴∠QOB=∠POQ=60°,
又∵PO=OQ,
∴PO=OQ=PQ,
∴∠QOB=∠PQO=60°,
∴PQ∥AB,
∴S△CPQ=S△POQ,
∴S阴影=S扇形POQ=$\frac{60×π×{3}^{2}}{360}$=$\frac{3}{2}π$(cm2),
故阴影部分面积为$\frac{3}{2}π$cm2.
点评 本题主要考查了等边三角形的判定与性质以及扇形的面积.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
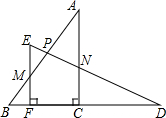 将两个全等的直角三角板ABC和DEF摆成如图形式,使点B,F,C,D在同一条直线上.
将两个全等的直角三角板ABC和DEF摆成如图形式,使点B,F,C,D在同一条直线上.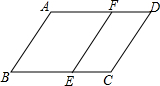 如图,∠B+∠C=180°,∠A=∠DFE,能得到EF∥CD吗?为什么?
如图,∠B+∠C=180°,∠A=∠DFE,能得到EF∥CD吗?为什么?
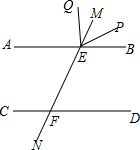 如图所示,已知直线AB,CD被直线MN所截,分别交于E,F,从E点引出两条射线EP,EQ,且满足∠PEQ=∠EFD,∠BEP=∠MEQ,直线AB,CD是否平行?为什么?
如图所示,已知直线AB,CD被直线MN所截,分别交于E,F,从E点引出两条射线EP,EQ,且满足∠PEQ=∠EFD,∠BEP=∠MEQ,直线AB,CD是否平行?为什么?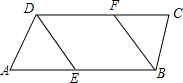 如图,已知∠ABC=∠ADC,BF、DE分别平分∠ABC,∠ADC,且∠AED=∠ABF,求证:∠A=∠C.
如图,已知∠ABC=∠ADC,BF、DE分别平分∠ABC,∠ADC,且∠AED=∠ABF,求证:∠A=∠C.