题目内容
11．
如图，为了估算河的宽度，我们可以在河对岸选定一个目标点A，再在河岸的这一边选取点B和点C，使AB⊥BC，然后再选取点E，使EC⊥BC，用视线确定BC和AE的交点D，此时如果测得BD=160m，DC=80m，EC=50m，求A、B间的大致距离．
分析 根据题意得出△ABD∽△ECD，进而利用相似三角形的性质得出AB的长．
解答 解：由题意可得：∠ABD=∠ECD=90°，∠ADB=∠EDC，
则△ABD∽△ECD，
故$\frac{BD}{DC}$=$\frac{AB}{EC}$，
即$\frac{160}{80}$=$\frac{AB}{50}$，
解得：AB=100．
答：A、B间的距离为100m．
点评 此题主要考查了相似三角形的应用，根据题意得出相似三角形是解题关键．
练习册系列答案
相关题目
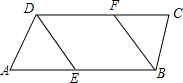如图，已知∠ABC=∠ADC，BF、DE分别平分∠ABC，∠ADC，且∠AED=∠ABF，求证：∠A=∠C．
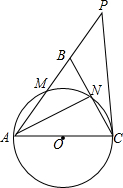如图，在△ABC中，∠ABC=∠ACB，以AC为直径的⊙O分别交AB、BC于点M、N，点P在AB的延长线上，且∠CAB=2∠BCP．
16．“$\frac{16}{49}$的平方根是±$\frac{4}{7}$”用数学式表示为（ ）
| A． | $\sqrt{\frac{16}{49}}$=±$\frac{4}{7}$ | B． | $\sqrt{\frac{16}{49}}$=$\frac{4}{7}$ | C． | ±$\sqrt{\frac{16}{49}}$=±$\frac{4}{7}$ | D． | -$\sqrt{\frac{16}{49}}$=-$\frac{4}{7}$ |
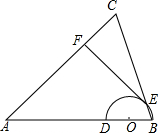已知：如图，在△ABC中，AB=AC，点O在边AB上，半圆O过点B，且分别与边AB、BC交于点D、E，点D与点A不重合，EF⊥AC，垂足为F．