题目内容
7.成都一机械长接到生产一批机器设备的订单,要求必须在12天(含12天)内完成.已知每台机械设备的成本价为800元,该长平时每天能生产该设备20台.为了加快进度,该厂采取工人分批日夜加班的方式,每天的生产量得到了提高.这样,第一天生产了22台,以后每天生产的设备都比前一天多2台.但由于机器损耗等原因,当每天生产的设备达到30台后,每多生产1台机械设备,当天生产的所有生产的设备每台的成本就增加20元.设生产这批设备的时间为x天,每天生产的机械设备为y台.(1)直接写出y与x之间的函数关系式,并写出自变量x的取值范围.
(2)若这批机器设备订购价格为每台1200元,该机械厂决定把获得最高利润的那一天的全部利润用来补贴困难职工.设该厂每天的利润为w元,试求出w与x之间的函数关系式,并求出该机械厂用来补贴给困难职工多少钱?
分析 本题是实际问题与一次函数、二次函数的综合运用,同时穿插着分段函数,需要由易到难,逐步求解;基本等量关系是:利润=(每台设备订购价-每台设备成本价-增加的其他费用)×生产量.
解答 解:(1)y=2x+20(1≤x≤12);
(2)当1≤x≤5时,W=(1200-800)×(2x+20)=800x+8000,
此时W随着x的增大而增大,
∴当x=5时,W最大值=12000;
当5<x≤12时,
W=[1200-800-20×(2x+20-30)]×(2x+20)
=-80(x-2.5)2+12500,
此时函数图象开口向下,在对称右侧,W随着x的增大而减小,又天数x为整数,
∴当x=6时,W最大值=11520元.
∵12000>11520,
∴当x=5时,W最大,且W最大值=12000元.
综上所述:
$w=\left\{\begin{array}{l}{800x+8000(1≤x≤5)}\\{-80(x-2.5)^{2}+12500(5<x≤12)}\end{array}\right.$.
∴该机械厂用来补贴给困难职工12000元.
点评 此题考查二次函数的应用,如何分段,怎样表达每个分段函数,并比较确定最大值,是解本题的关键.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
15.下列各数中,是方程x2=4x-3的解的是( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
2. 如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE,PF分别交AB,AC于点E,F,连接EF交AP于点G,给出以下五个结论:
如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE,PF分别交AB,AC于点E,F,连接EF交AP于点G,给出以下五个结论:
①∠B=∠C=45°;
②AE=CF,
③AP=EF,
④△EPF是等腰直角三角形,
⑤四边形AEPF的面积是△ABC面积的一半.
其中正确的结论是( )
 如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE,PF分别交AB,AC于点E,F,连接EF交AP于点G,给出以下五个结论:
如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE,PF分别交AB,AC于点E,F,连接EF交AP于点G,给出以下五个结论:①∠B=∠C=45°;
②AE=CF,
③AP=EF,
④△EPF是等腰直角三角形,
⑤四边形AEPF的面积是△ABC面积的一半.
其中正确的结论是( )
| A. | 只有① | B. | ①②④ | C. | ①②③④ | D. | ①②④⑤ |
17.若分式$\frac{1}{x-2}$有意义,则x的取值范围是( )
| A. | x>2 | B. | x<2 | C. | x≠2 | D. | x≠0 |

 有一张地图,有A、B、C三地,但地图被墨迹污染,C地具体位置看不清楚了,但知道C地在A地的北偏东30°,在B地的南偏东45°,你能帮他确定C地的位置吗?
有一张地图,有A、B、C三地,但地图被墨迹污染,C地具体位置看不清楚了,但知道C地在A地的北偏东30°,在B地的南偏东45°,你能帮他确定C地的位置吗?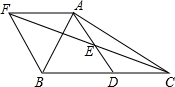 如图,在△ABC中,D是BC的中点,E是AD的中点,过点A作AF∥BC,AF与CE的延长线相交于点F,连接BF.
如图,在△ABC中,D是BC的中点,E是AD的中点,过点A作AF∥BC,AF与CE的延长线相交于点F,连接BF.