题目内容
2. 如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE,PF分别交AB,AC于点E,F,连接EF交AP于点G,给出以下五个结论:
如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE,PF分别交AB,AC于点E,F,连接EF交AP于点G,给出以下五个结论:①∠B=∠C=45°;
②AE=CF,
③AP=EF,
④△EPF是等腰直角三角形,
⑤四边形AEPF的面积是△ABC面积的一半.
其中正确的结论是( )
| A. | 只有① | B. | ①②④ | C. | ①②③④ | D. | ①②④⑤ |
分析 根据等腰直角三角形的性质得:∠B=∠C=45°,AP⊥BC,AP=$\frac{1}{2}$BC,AP平分∠BAC.所以可证∠C=∠EAP;∠FPC=∠EPA;AP=PC.即证得△APE与△CPF全等.根据全等三角形性质判断结论是否正确,根据全等三角形的面积相等可得△APE的面积等于△CPF的面积相等,然后求出四边形AEPF的面积等于△ABC的面积的一半.
解答 解:∵AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,
∴①∠B=∠C=$\frac{1}{2}$×(180°-90°)=45°,AP⊥BC,AP=$\frac{1}{2}$BC=PC,∠BAP=∠CAP=45°=∠C,
∵∠APF+∠FPC=90°,∠APF+∠APE=90°,
∴∠FPC=∠EPA.
∴△APE≌△CPF(ASA),
∴②AE=CF;④EP=PF,即△EPF是等腰直角三角形;同理可证得△APF≌△BPE,
∴⑤四边形AEPF的面积是△ABC面积的一半,
∵△ABC是等腰直角三角形,P是BC的中点,
∴AP=$\frac{1}{2}$BC,
∵EF不是△ABC的中位线,
∴EF≠AP,故③错误;
④∵∠AGF=∠EGP=180°-∠APE-∠PEF=180°-∠APE-45°,
∠AEP=180°-∠APE-∠EAP=180°-∠APE-45°,
∴∠AEP=∠AGF.
故正确的有①、②、④、⑤,共四个.
因此选D.
点评 本题考查了等腰直角三角形的性质的运用,全等三角形的判定及性质的运用,中位线的性质的运用,等腰直角三角形的判定定理的运用,三角形面积公式的运用,解答时灵活运用等腰直角三角形的性质求解是关键.

练习册系列答案
相关题目
14.目前,全球淡水资源日益减少,提倡全社会节约用水已成为全球的共识.据测试:拧不紧的水龙头每分钟滴出60滴水,每滴水约0.05毫升.小康洗手后,没有把水龙头拧紧,水龙头以测试的速度滴水.设小康离开x分钟后,水龙头滴出y毫升的水,则y与x之间的关系式是( )
| A. | y=0.05x | B. | y=3x | C. | y=60x | D. | y=0.05x+60 |
 如图,?ABCD中,点O是AC与BD的交点,过点O的直线与BA、DC的延长线分别交于点E、F.
如图,?ABCD中,点O是AC与BD的交点,过点O的直线与BA、DC的延长线分别交于点E、F.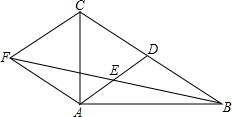 如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作AF∥BC,交BE的延长线于点F,连接CF.
如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作AF∥BC,交BE的延长线于点F,连接CF. 如图,已知梯形.
如图,已知梯形.