题目内容
19．$\left\{\begin{array}{l}{x+y=2}\\{y+z=4}\\{z+x=6}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=2}\\{y=0}\\{z=4}\end{array}\right.$．分析 根据解三元一次方程组的方法可以解答此方程，本题得以解决．
解答 解：$\left\{\begin{array}{l}{x+y=2}&{①}\\{y+z=4}&{②}\\{z+x=6}&{③}\end{array}\right.$，
①+②+③，得
x+y+z=6，④
④-①，得z=4，
④-②，得x=2，
④-③，得y=0，
故原方程组的解是$\left\{\begin{array}{l}{x=2}\\{y=0}\\{z=4}\end{array}\right.$．
点评 本题考查三元一次方程组的解，解得关键是明确解三元一次方程组的解答方法．
练习册系列答案
相关题目
9．
如图，已知AC⊥AB，∠1=30°，则∠2的度数是（ ）
如图，已知AC⊥AB，∠1=30°，则∠2的度数是（ ）| A． | 40° | B． | 50° | C． | 60° | D． | 70° |
如图，?ABCD中，点O是AC与BD的交点，过点O的直线与BA、DC的延长线分别交于点E、F．
14．目前，全球淡水资源日益减少，提倡全社会节约用水已成为全球的共识．据测试：拧不紧的水龙头每分钟滴出60滴水，每滴水约0.05毫升．小康洗手后，没有把水龙头拧紧，水龙头以测试的速度滴水．设小康离开x分钟后，水龙头滴出y毫升的水，则y与x之间的关系式是（ ）
| A． | y=0.05x | B． | y=3x | C． | y=60x | D． | y=0.05x+60 |
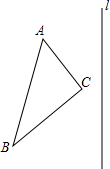作图题，用直尺和圆规按下列要求作图．
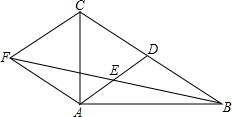如图，在△ABC中，AD是BC边上的中线，E是AD的中点，过点A作AF∥BC，交BE的延长线于点F，连接CF．
某中学部分同学参加全国初中数学竞赛，取得了优异的成绩，指导老师统计所有参赛同学的成绩（成绩都是整数，试题满分120分），并且绘制了频率分布直方图（如图）．请回答：