题目内容
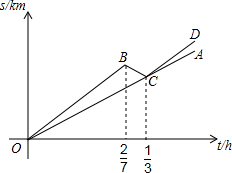 某自行车队根据队员速度的不同,分为快1组、快2组、慢1组和慢2组四个小组,在该车队的一次训练中,快1组和慢1组从甲地行进到乙地,剩下的组从乙地行进到甲地.快1组和慢1组同时从甲地出发,快1组的队员以高于慢1组队员10km/h的速度前行,快1组行驶一段时间后因某些原因又往回行驶(在往返过程中速度不变),最终与慢1组汇合,汇合后两组继续以各自的速度向乙地行进.设快1组和慢1组行驶的时间为t,与甲地的距离为s,s与t之间的函数图象如图所示.
某自行车队根据队员速度的不同,分为快1组、快2组、慢1组和慢2组四个小组,在该车队的一次训练中,快1组和慢1组从甲地行进到乙地,剩下的组从乙地行进到甲地.快1组和慢1组同时从甲地出发,快1组的队员以高于慢1组队员10km/h的速度前行,快1组行驶一段时间后因某些原因又往回行驶(在往返过程中速度不变),最终与慢1组汇合,汇合后两组继续以各自的速度向乙地行进.设快1组和慢1组行驶的时间为t,与甲地的距离为s,s与t之间的函数图象如图所示.(1)求OA解析式;
(2)已知甲地到乙地的距离为90km,在快1组与慢1组汇合时,慢2组(慢2组的速度与慢1组相同)由乙地开始出发,经过一段时间后,快1组合慢2组同时到达补给站.
①求此时慢2组与甲地之间的距离;
②若快2组在某一时刻也从乙地出发,速度与快1组相同,如果快2组不能比慢2组晚到甲地,求快2组比慢2组最多晚出发多少小时?
考点:一次函数的应用
专题:
分析:(1)由题意可知快1组的队员的速度比慢1组队员的速度每小时快10km,由图象可求出快1组的队员
小时比慢1组队员多行驶的路程为
×10=
,从而可求得快1组从返回到与慢1组汇合,两组共行驶的路程为
,由此设快1组的速度为xkm/h,则慢1组的速度为(x-10)km/h,则可列出方程,解得x的值,从而求得两组的速度,即可求得点C的坐标,再利用待定系数法求得OA的解析式;(2)①由题意可得慢2组从乙地出发时快1组与甲地的距离为
×25=
,从而可求得快1组与慢2组此时的距离为90-
=
,再利用相遇问题解法求得慢2组与快1组相遇时行驶的时间,从而求得慢2组行驶的路程,即可得到与甲地间的距离;②求出慢2组到甲地所用时间和快2组到甲地所用时间,相减即可得到答案.
| 2 |
| 7 |
| 2 |
| 7 |
| 20 |
| 7 |
| 20 |
| 7 |
| 1 |
| 3 |
| 25 |
| 3 |
| 25 |
| 3 |
| 245 |
| 3 |
解答:解:(1)∵快1组的队员的速度比慢1组队员的速度每小时快10km,
∴快1组的队员
小时比慢1组队员多行驶的路程为
×10=
km,
设快1组的速度为xkm/h,则慢1组的速度为(x-10)km/h,则可列出方程为:
(
-
)x+(
-
)(x-10)=
,
解得,x=35,x-10=25,
∴快1组的速度为35km/h,则慢1组的速度为25km/h,
∴
×25=
km,
∴点C的坐标为(
,
),
设OA的解析式为s=kt,把(
,
)代入得,
=
k,
解得,k=25,
∴OA的解析式为s=25t;
(2)①由(1)知慢2组的速度为25km/h,
∵慢2组与快1组相遇时行驶的时间为(90-
×25)÷(35+25)=
小时,
∴此时慢2组与甲地之间的距离为90-25×
=55
km,
②快2组比慢2组最多晚出发时间为:
-
=
小时.
∴快1组的队员
| 2 |
| 7 |
| 2 |
| 7 |
| 20 |
| 7 |
设快1组的速度为xkm/h,则慢1组的速度为(x-10)km/h,则可列出方程为:
(
| 1 |
| 3 |
| 2 |
| 7 |
| 1 |
| 3 |
| 2 |
| 7 |
| 20 |
| 7 |
解得,x=35,x-10=25,
∴快1组的速度为35km/h,则慢1组的速度为25km/h,
∴
| 1 |
| 3 |
| 25 |
| 3 |
∴点C的坐标为(
| 1 |
| 3 |
| 25 |
| 3 |
设OA的解析式为s=kt,把(
| 1 |
| 3 |
| 25 |
| 3 |
| 25 |
| 3 |
| 1 |
| 3 |
解得,k=25,
∴OA的解析式为s=25t;
(2)①由(1)知慢2组的速度为25km/h,
∵慢2组与快1组相遇时行驶的时间为(90-
| 1 |
| 3 |
| 49 |
| 36 |
∴此时慢2组与甲地之间的距离为90-25×
| 49 |
| 36 |
| 35 |
| 36 |
②快2组比慢2组最多晚出发时间为:
| 90 |
| 25 |
| 90 |
| 35 |
| 36 |
| 35 |
点评:本题考查了一次函数的应用,利用了函数与自变量的关系,一元一次方程的应用,题目稍有难度.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
太阳中心的温度高达19200000℃,有科学记数法将19200000℃可表示为( )
| A、1.92×106 |
| B、1.92×107 |
| C、19.2×106 |
| D、19.2×107 |
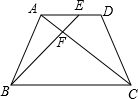 在等腰梯形ABCD中,AD∥CB,且AD=
在等腰梯形ABCD中,AD∥CB,且AD=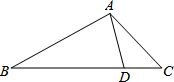 如图,在△ABC中,AC=4,AB=6,BC=8,点D在BC边上,且CD=2,则AD的长为
如图,在△ABC中,AC=4,AB=6,BC=8,点D在BC边上,且CD=2,则AD的长为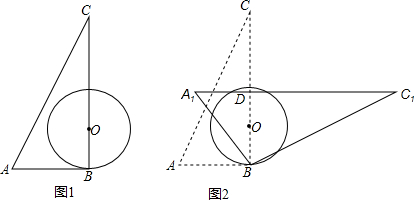
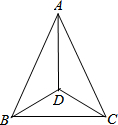 如图,已知在△ABC中,AB=AC,点D是△ABC内一点,且∠ABD=∠ACD,求证:AD是∠BAC的平分线.
如图,已知在△ABC中,AB=AC,点D是△ABC内一点,且∠ABD=∠ACD,求证:AD是∠BAC的平分线.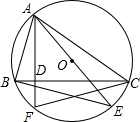 如图,△ABC是⊙O的内接三角形,AE是⊙O的直径,AF是⊙O的弦,且AF⊥BC于D点.求证:
如图,△ABC是⊙O的内接三角形,AE是⊙O的直径,AF是⊙O的弦,且AF⊥BC于D点.求证: 数):
数):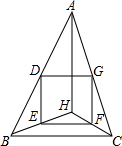 如图,锐角△ABC中,点H是三条高的交点,点D、E、F、G分别是AB、BH、CH、AC的中点.
如图,锐角△ABC中,点H是三条高的交点,点D、E、F、G分别是AB、BH、CH、AC的中点.