题目内容
解方程
(1)x2+4x-1=0
(2)3x2-5x-1=0.
(1)x2+4x-1=0
(2)3x2-5x-1=0.
考点:解一元二次方程-公式法,解一元二次方程-配方法
专题:
分析:(1)利用配方法(将一元二次方程配成(x+m)2=n的形式,再利用直接开平方法求解)和公式法解答都可以.
(2)利用求根公式进行解答即可.
(2)利用求根公式进行解答即可.
解答:解:(1)解法一:移项得:x2+4x=1
配方得:x2+4x+4=1+4
即(x+2)2=5
开方得:x+2=±
,
解得:x1=-2+
,x2=-2-
;
解法二:这里a=1,b=4,c=-1,
b2-4ac=16+4=20,
x=
,
解得 x1=-2+
,x2=-2-
;
(2)这里a=3,b=-5,c=-1,
b2-4ac=25+12=37,
x=
,
解得 x1=
,x2=
.
配方得:x2+4x+4=1+4
即(x+2)2=5
开方得:x+2=±
| 5 |
解得:x1=-2+
| 5 |
| 5 |
解法二:这里a=1,b=4,c=-1,
b2-4ac=16+4=20,
x=
-4±
| ||
| 2 |
解得 x1=-2+
| 5 |
| 5 |
(2)这里a=3,b=-5,c=-1,
b2-4ac=25+12=37,
x=
5±
| ||
| 6 |
解得 x1=
5+
| ||
| 6 |
5-
| ||
| 6 |
点评:本题考查了解一元二次方程的方法,当把方程通过移项把等式的右边化为0后方程的左边能因式分解时,一般情况下是把左边的式子因式分解,再利用积为0的特点解出方程的根.因式分解法是解一元二次方程的一种简便方法,要会灵活运用.当化简后不能用分解因式的方法即可考虑求根公式法,此法适用于任何一元二次方程.

练习册系列答案
相关题目
下列几组数不能作为直角三角形的三边长的是( )
| A、3,4,5 |
| B、4,8,10 |
| C、7,24,25 |
| D、8,15,17 |
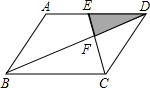 如图,平行四边形ABCD中,E为AD的中点,已知△DEF的面积为S,则△BCF的面积为( )
如图,平行四边形ABCD中,E为AD的中点,已知△DEF的面积为S,则△BCF的面积为( )| A、S | B、2S | C、3S | D、4S |
太阳中心的温度高达19200000℃,有科学记数法将19200000℃可表示为( )
| A、1.92×106 |
| B、1.92×107 |
| C、19.2×106 |
| D、19.2×107 |
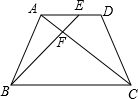 在等腰梯形ABCD中,AD∥CB,且AD=
在等腰梯形ABCD中,AD∥CB,且AD=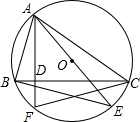 如图,△ABC是⊙O的内接三角形,AE是⊙O的直径,AF是⊙O的弦,且AF⊥BC于D点.求证:
如图,△ABC是⊙O的内接三角形,AE是⊙O的直径,AF是⊙O的弦,且AF⊥BC于D点.求证: