题目内容
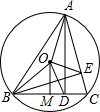 如图,锐角△ABC内接于圆O,AD⊥BC,BE⊥AC,OM⊥BC,垂足分别为D、E、M.
如图,锐角△ABC内接于圆O,AD⊥BC,BE⊥AC,OM⊥BC,垂足分别为D、E、M.(1)若∠ACB=60°,求∠ABO的大小;
(2)△OMB与△AEB相似吗?为什么?
(3)判断△OBD与△OAE的面积是否相等?并说明理由.
考点:相似三角形的判定与性质,圆周角定理
专题:
分析:(1)证明∠AOB=120°,∠BAO=∠ABO,即可解决问题.
(2)证明∠BOM=∠BAE;∠OMB=∠AEB=90°,即可解决问题.
(3)如图,作辅助线;证明△AON∽△ADB,得到
=
;证明
=
;运用OA=OB,得到
=
,进而得到OM•BD=ON•AE,得到
OM•BD=
ON•AE,即可解决问题.
(2)证明∠BOM=∠BAE;∠OMB=∠AEB=90°,即可解决问题.
(3)如图,作辅助线;证明△AON∽△ADB,得到
| OA |
| AB |
| ON |
| BD |
| OB |
| AB |
| OM |
| AE |
| ON |
| BD |
| OM |
| AE |
| 1 |
| 2 |
| 1 |
| 2 |
解答: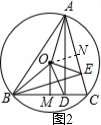
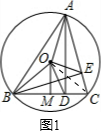 解:(1)如图,∵∠ACB=60°,
解:(1)如图,∵∠ACB=60°,
∴∠AOB=120°;而OA=OB,
∴∠BAO=∠ABO=
=30°,
即∠ABO=30°.
(2)相似;理由如下:
如图,连接OC,则OB=OC;
∵OM⊥BC,
∴∠BOM=
∠BOC,而∠BAC=
∠BOC,
∴∠BOM=∠BAE;而BE⊥AC,
∴∠OMB=∠AEB=90°,
∴△OMB∽△AEB.
(3)相等;理由如下:
如图,过点O作ON⊥AC于点N;
∵AO=CO,ON⊥AC,
∴∠AON=
∠AOC,而∠ABC=
∠AOC,
∴∠AON=∠ABC,而∠ONA=∠BNO,
∴△AON∽△ADB,
∴
=
;
同理可证:△OMB∽△AEB,
∴
=
;而OA=OB,
∴
=
,OM•BD=ON•AE,
∴
OM•BD=
ON•AE,
即△OBD与△OAE的面积相等.

 解:(1)如图,∵∠ACB=60°,
解:(1)如图,∵∠ACB=60°,∴∠AOB=120°;而OA=OB,
∴∠BAO=∠ABO=
| 180°-120° |
| 2 |
即∠ABO=30°.
(2)相似;理由如下:
如图,连接OC,则OB=OC;
∵OM⊥BC,
∴∠BOM=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BOM=∠BAE;而BE⊥AC,
∴∠OMB=∠AEB=90°,
∴△OMB∽△AEB.
(3)相等;理由如下:
如图,过点O作ON⊥AC于点N;
∵AO=CO,ON⊥AC,
∴∠AON=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠AON=∠ABC,而∠ONA=∠BNO,
∴△AON∽△ADB,
∴
| OA |
| AB |
| ON |
| BD |
同理可证:△OMB∽△AEB,
∴
| OB |
| AB |
| OM |
| AE |
∴
| ON |
| BD |
| OM |
| AE |
∴
| 1 |
| 2 |
| 1 |
| 2 |
即△OBD与△OAE的面积相等.
点评:该题主要考查了圆周角定理、相似三角形的判定及其性质等几何知识点及其应用问题;解题的关键是牢固掌握定理本质内容,这是灵活运用解题的基础和关键.

练习册系列答案
相关题目
太阳中心的温度高达19200000℃,有科学记数法将19200000℃可表示为( )
| A、1.92×106 |
| B、1.92×107 |
| C、19.2×106 |
| D、19.2×107 |
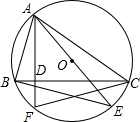 如图,△ABC是⊙O的内接三角形,AE是⊙O的直径,AF是⊙O的弦,且AF⊥BC于D点.求证:
如图,△ABC是⊙O的内接三角形,AE是⊙O的直径,AF是⊙O的弦,且AF⊥BC于D点.求证: 数):
数):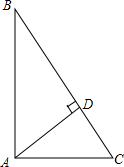 如图,在△ABC中,∠BAC=90°,AD⊥BC,AB=4,DC=
如图,在△ABC中,∠BAC=90°,AD⊥BC,AB=4,DC=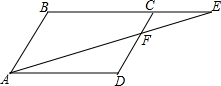 如图,四边形ABCD为?,BC=2CE,则S△CEF:S四边形ABCD=
如图,四边形ABCD为?,BC=2CE,则S△CEF:S四边形ABCD=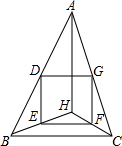 如图,锐角△ABC中,点H是三条高的交点,点D、E、F、G分别是AB、BH、CH、AC的中点.
如图,锐角△ABC中,点H是三条高的交点,点D、E、F、G分别是AB、BH、CH、AC的中点. 如图,在4×7的点阵中任两点竖直或水平相邻的点都相距1个单位长度,已知线段AB交线段CD于点E,试求出线段AE的长.
如图,在4×7的点阵中任两点竖直或水平相邻的点都相距1个单位长度,已知线段AB交线段CD于点E,试求出线段AE的长.