题目内容

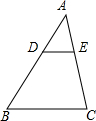如图，DE∥BC，AD：DB=2：3，则△AED和△ABC的相似比为
 
．
考点：相似三角形的判定与性质
专题：
分析：由AD：DB=2：3，设AD=2x，BD=3x，就可以得出AB=5x，由DE∥BC就可以得出△AED∽△ABC就可以得出结论．
解答：解：∵AD：DB=2：3，设AD=2x，BD=3x，
∴AB=5x．
∵DE∥BC，
∴△AED∽△ABC，
∴
AD
AB
=
2
5
．
故答案为：
2
5
．
点评：本题考查了比例的运用，相似三角形的判定及性质的运用，解答时证明三角形的相似是关键．
练习册系列答案
相关题目
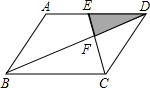如图，平行四边形ABCD中，E为AD的中点，已知△DEF的面积为S，则△BCF的面积为（　　）
A、SB、2SC、3SD、4S
如图，一张直角三角形硬纸片ABC，∠B=90°，AB=5，AC=13，将纸片顶点B放在半径为2.4的⊙O上，并使BC经过圆心O，在⊙O不动的情况下，将纸片绕着B按顺时针方向旋转．
（1）当旋转角的度数等于∠A的度数时，得到△A1BC1，问直线A1C1与⊙O有怎样的位置关系？为什么？
（2）在（1）的状态下，再继续旋转∠C的度数，得到△A2BC2，那么A2C2与⊙O的位置关系是否发生变化？通过计算或推理说明你的理由．
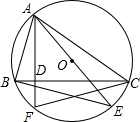如图，△ABC是⊙O的内接三角形，AE是⊙O的直径，AF是⊙O的弦，且AF⊥BC于D点．求证：
（1）△ADC∽△ABE； 
（2）BE=CF．
已知直线y=-x+1交x，y轴于A，B两点，反比例函数y=
k
x
在第一象限内的图象上有点P，连AP，BP且四边形OAPB是正方形．
①求反比例函数的解析式；
②若动点P在双曲线上运动，作PM⊥x轴交AB于E点；PN⊥y轴交AB于F点．以下有两个结论：AF与BE的积不变，AF与BE的商不变，其中有一个是正确的，请选出正确的结论，并加以证明．
“十一”黄金周期间，刘公岛景区在7天假期中每天接待的旅游人数变化情况如表（正数表示比前一天多的人数，负数表示比前一天少的人数）：
日期1日2日3日4日5日6日7日
人数变化单位：万人+1.6+0.8+0.4-0.4-0.6+0.2-1.2
（1）若9月30日的游客人数为5万人，则10月2日的游客人数是
 
万人；
（2）七天内游客人数最多的是
 
日，最少的是
 
日．
（3）以9月30日的游客人数为0点，用折线统计图表示这7天的游客人数变化情况．
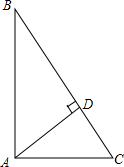如图，在△ABC中，∠BAC=90°，AD⊥BC，AB=4，DC=
9
5
，求sinC的值．
从甲、乙两位运动员中选出一名参加在规定时间内的投篮比赛．预先对这两名运动员进行了6次测试，成绩如下（单位：个）：
甲：6，12，8，12，10，12；
乙：9，10，11，10，12，8；
（1）填表：
平均数众数方差
甲10
 
 
乙
 
10
5
3
（2）根据测试成绩，请你运用所学的统计知识作出分析，派哪一位运动员参赛更好？为什么？
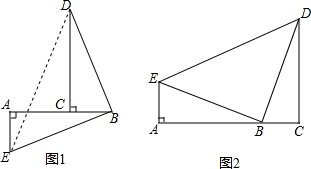已知C点是直线AB上的一动点．
（1）如图1，当C在线段AB上运动时，作DC⊥AB，垂足为C，EA⊥AB，垂足为A，且DC=AB，AE=BC．连接DE，判断△BDE的形状，并说明理由；
（2）如图2，当C在线段AB的延长线上运动时，作DC⊥AB，垂足为C，EA⊥AB，垂足为A，且DC=AB，AE=BC．连接DE，判断△BDE的形状，并说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网