题目内容
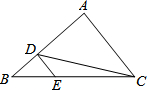如图，在△ABC中，D，E分别是AB，BC上的点，且DE∥AC，若S△BDE：S△CDE=1：3，则S△BDE：S△ACD=（ ）| A、1：5 | B、1：9 |
| C、1：10 | D、1：12 |
考点：相似三角形的判定与性质
专题：
分析：设△BDE的面积为a，表示出△CDE的面积为3a，根据等高的三角形的面积的比等于底边的比求出
，然后求出△DBE和△ABC相似，根据相似三角形面积的比等于相似比的平方求出△ABC的面积，然后表示出△ACD的面积，再求出比值即可．
| BE |
| CE |
解答：解：∵S△BDE：S△CDE=1：3，
∴设△BDE的面积为a，则△CDE的面积为3a，
∵△BDE和△CDE的点D到BC的距离相等，
∴
=
，
∴
=
，
∵DE∥AC，
∴△DBE∽△ABC，
∴S△DBE：S△ABC=1：16，
∴S△ACD=16a-a-3a=12a，
∴S△BDE：S△ACD=a：12a=1：12．
故选：D．
∴设△BDE的面积为a，则△CDE的面积为3a，
∵△BDE和△CDE的点D到BC的距离相等，
∴
| BE |
| CE |
| 1 |
| 3 |
∴
| BE |
| BC |
| 1 |
| 4 |
∵DE∥AC，
∴△DBE∽△ABC，
∴S△DBE：S△ABC=1：16，
∴S△ACD=16a-a-3a=12a，
∴S△BDE：S△ACD=a：12a=1：12．
故选：D．
点评：本题考查了相似三角形的判定与性质，等高的三角形的面积的比等于底边的比，熟记相似三角形面积的比等于相似比的平方，用△BDE的面积表示出△ABC的面积是解题的关键．
练习册系列答案
相关题目
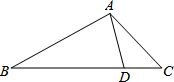如图，在△ABC中，AC=4，AB=6，BC=8，点D在BC边上，且CD=2，则AD的长为
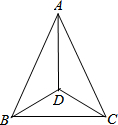如图，已知在△ABC中，AB=AC，点D是△ABC内一点，且∠ABD=∠ACD，求证：AD是∠BAC的平分线．
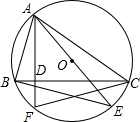如图，△ABC是⊙O的内接三角形，AE是⊙O的直径，AF是⊙O的弦，且AF⊥BC于D点．求证：
数）：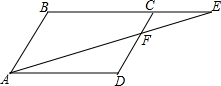
如图，四边形ABCD为?，BC=2CE，则S△CEF：S四边形ABCD=
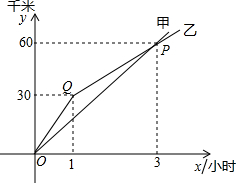自行车运动员甲、乙在公路上进行训练．如图，是反映他们在训练过程中的行驶路程（千米）和行驶时间（小时）之间的部分图象．