题目内容
13．设A、B、C、D、E都是整数，且有|A-B|=19，|B-C|=7，|C-D|=5，|D-E|=4，|E-A|=11，又A+B+C+D+E=56，求E．分析 先根据绝对值的性质得到A=B±19，B=C±7，C=D±5，D=E±4，E=A±11 从而得到A+B+C+D+E=B±19+C±7+D±5+E±4+A±11，所以A+B+C+D+E=（A+B+C+D+E）±19±7±5±4±11，要满足±19±7±5±4±11=0，取+19-7-5+4-11=0，所以A=B+19，B=C-7，C=D-5，D=E+4，E=A-11，即A=E+11，B=E-8，C=E-1，D=E+4，即可解答．
解答 解：|A-B|=19，|B-C|=7，|C-D|=5，|D-E|=4，|E-A|=11
所以 A=B±19，B=C±7，C=D±5，D=E±4，E=A±11
所以A+B+C+D+E=B±19+C±7+D±5+E±4+A±11
A+B+C+D+E=（A+B+C+D+E）±19±7±5±4±11
所以要满足（±19）+（±7）+（±5）+（±4）+（±11）=0，
所以取+19-7-5+4-11=0
所以A=B+19，B=C-7，C=D-5，D=E+4，E=A-11
即A=E+11，B=E-8，C=E-1，D=E+4
所以E+11+E-8+E-1+E+4+E=56
解得E=10．
点评 本题考查了绝对值，解决本题的关键是熟记绝对值的性质．
练习册系列答案
相关题目
4．
如图，正方形ABCD中，E是BC边上一点，以E为圆心，EC为半径的半圆与以A为圆心，AB为半径的圆弧外切，则tan∠EAB的值是（ ）
如图，正方形ABCD中，E是BC边上一点，以E为圆心，EC为半径的半圆与以A为圆心，AB为半径的圆弧外切，则tan∠EAB的值是（ ）| A． | $\frac{\sqrt{3}}{2}$ | B． | $\frac{\sqrt{3}}{3}$ | C． | $\frac{3}{4}$ | D． | $\frac{1}{2}$ |
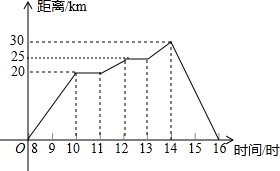假日里，小亮和爸爸骑自行车郊游，上午8时从家出发，16时返回家中，他们离家的距离与时间的关系可用图中的折线表示．