题目内容
2．已知一个矩形的宽是长的一半，对角线长为3$\sqrt{5}$，则该矩形的面积为18．分析 设矩形的宽AB=x，则BC=2x，由勾股定理得出方程，解方程求出AB、BC，矩形ABCD的面积=AB•BC，即可得出结果．
解答 解：如图所示：
∵四边形ABCD是矩形，
∴∠ABC=90°，AB=CD，AD=BC，
设矩形的宽AB=x，则BC=2x，
由勾股定理得：AB2+BC2=AC2，
即x2+（2x）2=（3$\sqrt{5}$）2，
解得：x=3，
∴2x=6，
∴AB=3，BC=6，
∴矩形ABCD的面积=AB•BC=3×6=18；
故答案为：18．
点评 本题考查了矩形的性质、勾股定理、矩形面积的计算方法；熟练掌握矩形的性质，并能进行推理计算是解决问题的关键．
练习册系列答案
相关题目
如图，矩形ABCD中，AB=6cm，BC=8cm，点P在AD边上移动（不与点A、D重合），过点C作BP的垂线，垂足为点Q．设BP的长为xcm，CQ的长为ycm，求y与x之间的函数关系式及自变量x的取值范围．
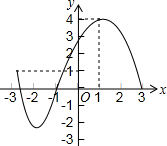已知某一函数的图象如图所示，根据图象回答下列问题：
如图所示，一架云梯AB斜靠在一面墙上，设木棍的中点为P．若木棍A端沿墙下滑，且B端沿底面向右滑行．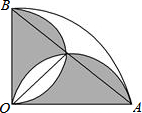
半径1cm，圆心角90度的扇形OAB中，分别以OA，OB为直径作半圆，则阴影部分（两个半圆除了重叠部分其余部分）面积为$\frac{1}{2}$．
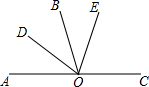已知，O是直线AC上一点，OD平分∠AOB，∠BOE=$\frac{1}{2}$∠EOC，∠DOE=72°，OB是∠DOE的平分线吗？说明理由．