题目内容
4. 如图,正方形ABCD中,E是BC边上一点,以E为圆心,EC为半径的半圆与以A为圆心,AB为半径的圆弧外切,则tan∠EAB的值是( )
如图,正方形ABCD中,E是BC边上一点,以E为圆心,EC为半径的半圆与以A为圆心,AB为半径的圆弧外切,则tan∠EAB的值是( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{2}$ |
分析 设切点为P,则AP=AD,EP=CE,根据已知利用勾股定理即可求得CE的长,从而即可得出∠EAB的正切值.
解答 解:∵两圆弧外切 ,
,
∴AE的长即为两圆的半径之和;
设切点为P,正方形ABCD的边长是4k,则AP=AD,EP=CE,
在Rt△ABE中,由勾股定理列出方程AB2+(BC-CE)2=(AP+EP)2,
即(4k)2+(4k-CE)2=(4k+CE)2,
解得CE=k.
故BE=3k,
所以tan∠EAB的值是$\frac{3}{4}$.
故选C.
点评 此题考查两相切圆的性质以及正方形的性质,关键是先构建一个直角三角形,然后解直角三角函数即可.

练习册系列答案
相关题目
14.绝对值和相反数都是它本身的数是( )
| A. | 1 | B. | -1 | C. | 0 | D. | 所有正数 |
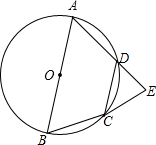 如图,四边形ABCD内接于⊙O,AB是⊙O的直径,BC=CD,CE⊥AD的延长线,垂足为E
如图,四边形ABCD内接于⊙O,AB是⊙O的直径,BC=CD,CE⊥AD的延长线,垂足为E
 如图,矩形ABCD中,AB=6cm,BC=8cm,点P在AD边上移动(不与点A、D重合),过点C作BP的垂线,垂足为点Q.设BP的长为xcm,CQ的长为ycm,求y与x之间的函数关系式及自变量x的取值范围.
如图,矩形ABCD中,AB=6cm,BC=8cm,点P在AD边上移动(不与点A、D重合),过点C作BP的垂线,垂足为点Q.设BP的长为xcm,CQ的长为ycm,求y与x之间的函数关系式及自变量x的取值范围.